


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with the Maple commands for triple integrals.
For last week's lab on double integrals, we calculated volume by integrating the differece between the upper function 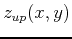 and the lower function
and the lower function 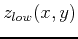 over a bounded two-dimensional region
over a bounded two-dimensional region 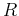 . We can also calculate volume using a triple integral using the lower and upper functions as the lower and upper bounds of the inner integral with respect to
. We can also calculate volume using a triple integral using the lower and upper functions as the lower and upper bounds of the inner integral with respect to 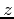 and
and 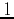 as the integrand. In many cases, we may need to evaluate a triple integral where the integrand is
as the integrand. In many cases, we may need to evaluate a triple integral where the integrand is 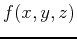 instead of 1. Although these integrals do not represent volume, the bounds on the integral are over a bounded 3-D region
instead of 1. Although these integrals do not represent volume, the bounds on the integral are over a bounded 3-D region 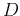 that can be set up the same way as a volume problem.
that can be set up the same way as a volume problem.
Given a mass density function 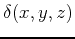 over a 3-D region
over a 3-D region 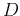 , the mass of the object is defined by
, the mass of the object is defined by
and the first moments of the solid region 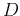 :
:
About the 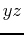 -plane is:
-plane is:
About the 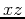 -plane is:
-plane is:
About the 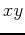 -plane is:
-plane is:
and the center of mass
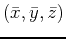 is:
is:
The following Maple commands show an example of a triple integral to calculate the volume of a hemisphere of radius 2 after solving 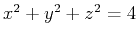 for
for 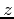 as a function of
as a function of 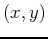 . If the mass density function is
. If the mass density function is
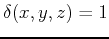 , then the mass is equivalent to the volume of the hemisphere and the
, then the mass is equivalent to the volume of the hemisphere and the 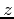 -coordinate for the center of mass can be calculated using the Maple commands shown below.
-coordinate for the center of mass can be calculated using the Maple commands shown below.
> with(plots):
> sphere := x^2+y^2+z^2=4
> implicitplot3d(sphere,x=-2..2,y=-2..2,z=0..2)
> M:=int(int(int(1,z=0..sqrt(4-x^2-y^2)),y=-sqrt(4-x^2)..sqrt(4-x^2)),x=-2..2)
> Mxy:=int(int(int(z,z=0..sqrt(4-x^2-y^2)),y=-sqrt(4-x^2)..sqrt(4-x^2)),x=-2..2)
> zbar:=Mxy/M
Volumes for some surfaces calculated as a triple integral can be drastically simplified by a change of coordinates. Just as polar coordinates simplify many two-dimensional area problems, cylindrical coordinates simplify many three-dimensional volume problems. The equations relating rectangular 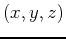 coordinates to cylindrical
coordinates to cylindrical 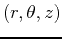 are:
are:
So, the hemisphere of radius 2 described above would have cylindrical coordinate equation 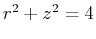 and the
and the 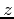 -coordinate for the center of mass can be calculated using a triple integral in spherical coordinates using the Maple commands shown below.
-coordinate for the center of mass can be calculated using a triple integral in spherical coordinates using the Maple commands shown below.
> with(plots):
> sphere_cylindrical := simplify(subs({x=r*cos(theta),y=r*sin(theta),z=z},sphere))
> implicitplot3d(r^2+z^2=4,r=0..2,theta=0..2*Pi,z=0..2,coords=cylindrical)
> solve(sphere_cylindrical,r)
> M:=int(int(int(r,z=0..sqrt(4-r^2)),r=0..2),theta=0..2*Pi)
> Mxy:=int(int(int(z*r,z=0..sqrt(4-r^2)),r=0..2),theta=0..2*Pi)
> zbar:=Mxy/M
- For the cylinder
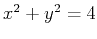 bounded by the planes
bounded by the planes 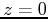 and
and 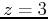 , with radius 2 and height 3,
, with radius 2 and height 3,
- a
- Use the implicitplot3d command with the first argument
![$\left[x^2+y^2 = 4, z = 0, z = 3\right]$](img31.png) and plotting ranges
and plotting ranges
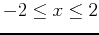 ,
,
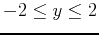 ,
,
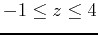 to generate a surface plot of the cylinder.
to generate a surface plot of the cylinder.
- b
- Show, using a triple integral that the volume is
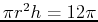 .
.
- c
- Assuming that the mass density function
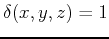 , use triple integrals to find the
, use triple integrals to find the 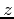 -coordinate for the center of mass. (Hint: the volume you found above is the mass, so label as
-coordinate for the center of mass. (Hint: the volume you found above is the mass, so label as 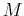 and using symmetry, you know that the center of mass should be
and using symmetry, you know that the center of mass should be
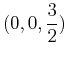 .
.
- d
- Show that the equation for the cylinder above in cylindrical coordinates is
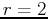 and generate a cylindrical coordinate plot of the surfaces given in part a.
and generate a cylindrical coordinate plot of the surfaces given in part a.
- e
- Find the volume/mass and the
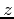 -coordinate for the center of mass using triple integrals in cylindrical coordinates.
-coordinate for the center of mass using triple integrals in cylindrical coordinates.
- For the cylinder
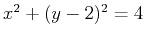 bounded by the planes
bounded by the planes 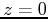 and
and 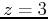 , also having radius 2 and height 3,
, also having radius 2 and height 3,
- a
- Use the implicitplot3d command with plotting ranges
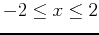 ,
,
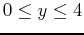 ,
,
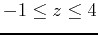 to generate a surface plot of the cylinder.
to generate a surface plot of the cylinder.
- b
- Show again, using a triple integral that the volume is
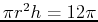 .
.
- c
- Assuming that the mass density function
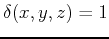 , use triple integrals to find the
, use triple integrals to find the 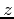 -coordinate for the center of mass. (Although the
-coordinate for the center of mass. (Although the 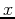 and
and 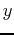 coordinates for the center of mass are different, the
coordinates for the center of mass are different, the 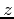 coordinate should be the same as the cylinder in exercise 1.)
coordinate should be the same as the cylinder in exercise 1.)
- d
- Show that the equation for the cylinder above in cylindrical coordinates is
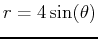 and generate a cylindrical coordinate plot of the surfaces given in part a.
and generate a cylindrical coordinate plot of the surfaces given in part a.
- e
- Find the volume/mass and the
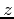 -coordinate for the center of mass using triple integrals in cylindrical coordinates.
-coordinate for the center of mass using triple integrals in cylindrical coordinates.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2018-12-02
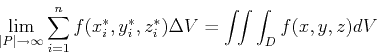
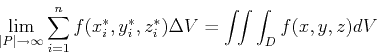
![]() for
for ![]() as a function of
as a function of ![]() . If the mass density function is
. If the mass density function is
![]() , then the mass is equivalent to the volume of the hemisphere and the
, then the mass is equivalent to the volume of the hemisphere and the ![]() -coordinate for the center of mass can be calculated using the Maple commands shown below.
-coordinate for the center of mass can be calculated using the Maple commands shown below.
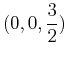 .
.