


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
To assist you, there is a worksheet associated with this lab that
contains examples and even solutions to some of the exercises. You can
copy that worksheet to your home directory by going to your computer's Start menu and choose run. In the run field type:
\\filer\calclab
when you hit enter, you can then choose MA1024 and then choose the worksheet
Coords_start_C12.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
Defining surfaces with rectangular coordinates often times becomes more complicated than necessary. A change in coordinates can simplify things. Cylindrical coordinates can simplify plotting a region in space that is symmetric with respect to the 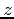 -axis such as paraboloids and cylinders. The paraboloid
-axis such as paraboloids and cylinders. The paraboloid 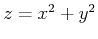 would become
would become 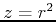 and the cylinder
and the cylinder 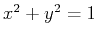 would become
would become 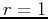 . Spherical coordinates would simplify the equation of a sphere, such as
. Spherical coordinates would simplify the equation of a sphere, such as 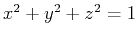 , to
, to 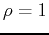 . The conversion tables below show how to make the change of coordinates.
. The conversion tables below show how to make the change of coordinates.
To change to cylindrical coordinates from rectangular coordinates use the conversion:
y
Where 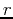 is the radius in the x-y plane and
is the radius in the x-y plane and 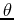 is the angle in the x-y plane.
is the angle in the x-y plane.
To change to spherical coordinates from rectangular coordinates use the conversion:
Where 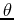 is the angle in the x-y plane;
is the angle in the x-y plane; 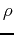 is the radius from the origin in any direction; and
is the radius from the origin in any direction; and 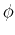 is the angle in the x-z plane.
is the angle in the x-z plane.
Using a triple integral to find the volume of a solid translates in the following manner:
- Given the rectangular equation for a circular cone:
- A)
- Graph the equation using the domain values of
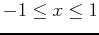 ,
,
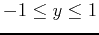 and the range values
and the range values
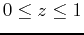 .
.
- B)
- Write the equation in cylindrical coordinates and then graph the equation.
- C)
- Write the equation in spherical coordinates and graph it.
- Use rectangular coordinates and a triple integral to find the volume of a right circular cone, given by the equation of the cone in exercise 1, of height
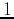 . Now repeat this using cylindrical coordinates. Which method is easier?
. Now repeat this using cylindrical coordinates. Which method is easier?
- Now suppose an ice cream cone is bounded below by the same equation of the cone given in exercise 1 and bounded above by the sphere
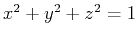 . Find the volume of the ice cream cone using spherical coordinates.
. Find the volume of the ice cream cone using spherical coordinates.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2012-02-20