\\filer\calclab
when you hit enter, you can then choose MA1024 and then choose the worksheet
Surf_start_C14.mw
Remember to immediately save it in your own home directory. Once you've copied and saved the worksheet, read through the background on the internet and the background of the worksheet before starting the exercises.
One of the most valuable services provided by computer software such as Maple is that it allows us to produce intricate graphs with a minimum of effort on our part. This becomes especially apparent when it comes to functions of two variables, because there are many more computations required to produce one graph, yet Maple performs all these computations with only a little guidance from the user.
The simplest way of describing a surface in Cartesian coordinates is
as the graph of a function ![]() over a domain, e.g. a set of
points in the
over a domain, e.g. a set of
points in the ![]() plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation
plane. The domain can have any shape, but a
rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as
the graph of an equation ![]() , where
, where ![]() is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface
is a constant. In
this case, we say the surface is defined implicitly. A third way of
representing a surface ![]() is through the use of level
curves. The idea is that a plane
is through the use of level
curves. The idea is that a plane ![]() intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the ![]() plane is
called a level curve. A collection of such curves for different values
of
plane is
called a level curve. A collection of such curves for different values
of ![]() is a representation of the surface called a contour plot.
Similar to the idea of level curves is to look at cross sections of the surface to see what two-dimensional shape is traced, not only in the
is a representation of the surface called a contour plot.
Similar to the idea of level curves is to look at cross sections of the surface to see what two-dimensional shape is traced, not only in the ![]() plane by letting
plane by letting ![]() be constant, but also in the
be constant, but also in the ![]() plane by holding
plane by holding ![]() constant and the
constant and the ![]() plane by holding
plane by holding ![]() constant.
constant.
Defining functions of two variables in Maple is very similar to the way it is done for functions of one variable - just remember the parentheses.
>f:=(x,y)->x^2+y^2;Evaluating the function at a specific (x,y) value is easy:
>f(3,1);
The plot3d command is similar to the plot command except the domain has both x and y values.However, there is a lot more you can do with plot3d. First try moving the plot by clicking and dragging. Also, a menu of options will appear if you right click on the graph.
>plot3d(f(x,y),x=-2..2,y=-2..2);Instead of using the right-click menu you can put the options into the plot command.
plot3d(f(x,y),x=-2..2,y=-2..2,scaling=constrained,axes=boxed,color=magenta);
The easiest way to get cross sections (parallel to the x-y plane) is to use the Maple command contourplot which is included in the package plots. The following command will show 15 cross sections using z-values that the computer will choose.
>with(plots): >contourplot(f(x,y),x=-2..2,y=-2..2,contours=15);Thefollowing command will show 4 cross sections using z-values that you choose.
>contourplot(f(x,y),x=-2..2,y=-2..2,contours=[-1,0,1,2]);In the above commands the z-value was held constant thus giving a two-dimensional plot. You can hold x or y constant to get a cross section perpendicular to the y-z or x-z plane. To get these cross sections use the plot command.
>plot(f(5,y),y=-2..2,labels=[y,z]);Note how easy it is to hold the x (or y) constant when you have entered a function, f(5,y). Also note that the axes were labeled to emphasize what the two remaining variables are. Next is an example of four contours parallel to the x-z plane.
>plot({f(x,-1),f(x,0),f(x,1),f(x,2)},x=-2..2,labels=[x,z]);
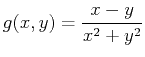 for the
for the