


Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to introduce you to some of the Maple
commands that can be used to plot surfaces in three dimensions.
To assist you, there is a worksheet associated with this lab that
contains examples to get you aquainted with the lab. You can copy that worksheet to your home directory with the following command, which must be run in a terminal window for example, not in Maple.
cp /math/calclab/MA1024/Surf_start.mws My_Documents
You can copy the worksheet now, but you should read through the lab before you load it into Maple. Once you have read to the exercises, start up Maple, load the worksheet Surf_start.mws, and go through it carefully. Then you can start working on the exercises.
The graph of a function of a single real variable is a set of points 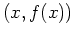 in the plane. Typically, the graph of such a function is a curve. For functions of two variables in Cartesian coordinates, the graph is a set of points
in the plane. Typically, the graph of such a function is a curve. For functions of two variables in Cartesian coordinates, the graph is a set of points 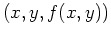 in three-dimensional space. For this reason, visualizing functions of two variables is usually more difficult.
in three-dimensional space. For this reason, visualizing functions of two variables is usually more difficult.
One of the most valuable services provided by computer software such as Maple is that it allows us to produce intricate graphs with a minimum of effort on our part. This becomes especially apparent when it comes to functions of two variables, because there are many more computations required to produce one graph, yet Maple performs all these computations with only a little guidance from the user.
The simplest way of describing a surface in Cartesian coordinates is as the graph of a function 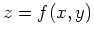 over a domain, e.g. a set of points in the
over a domain, e.g. a set of points in the 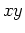 plane. The domain can have any shape, but a rectangular one is the easiest to deal with.
plane. The domain can have any shape, but a rectangular one is the easiest to deal with.
Another common, but more difficult way of describing a surface is as the graph of an equation 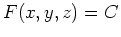 , where
, where 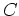 is a constant. In this case, we say the surface is defined implicitly. A third way of representing a surface
is a constant. In this case, we say the surface is defined implicitly. A third way of representing a surface 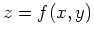 is through the use of level curves. The idea is that a plane
is through the use of level curves. The idea is that a plane 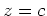 intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the 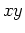 plane is called a level curve. A collection of such curves for different values of
plane is called a level curve. A collection of such curves for different values of 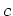 is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
Similar to the idea of level curves is to look at cross sections of the surface to see what two-dimensional shape is traced, not only in the 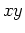 plane by letting
plane by letting 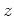 be constant, but also in the
be constant, but also in the 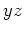 plane by holding
plane by holding 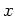 constant and the
constant and the 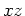 plane by holding
plane by holding 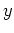 constant.
constant.
- For the given equations below, plot two dimensional level curves parallel to the
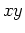 plane and then plot two dimensional cross sections in the
plane and then plot two dimensional cross sections in the 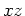 plane and the
plane and the 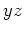 plane. Identify the type or shape of the quadric surface, ie. a sphere, cylinder, cone, elliptic cone, paraboloid, elliptic parabaloid, ellipsoid, hyperboloid of one sheet, hyperboloid of two sheets, elliptic hyperboloid of one or two sheets, or a hyperbolic parabaloid (saddle). Once you have determined the shape of the surface, supply a three dimensional plot to support your conclusion.
plane. Identify the type or shape of the quadric surface, ie. a sphere, cylinder, cone, elliptic cone, paraboloid, elliptic parabaloid, ellipsoid, hyperboloid of one sheet, hyperboloid of two sheets, elliptic hyperboloid of one or two sheets, or a hyperbolic parabaloid (saddle). Once you have determined the shape of the surface, supply a three dimensional plot to support your conclusion.
- a)
-
- b)
-
- c)
-
- Create a contour plot for the function
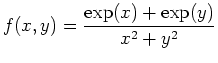 for the
for the 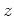 values
values 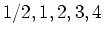 using two different methods; first using cross sections and then using Maple's contourplot command.
using two different methods; first using cross sections and then using Maple's contourplot command.
- Consider the following function
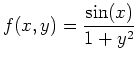 for
for
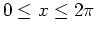 and
and
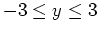 which looks like a deep valley with a mountain opposite it. Is is possible to find a path from the point
which looks like a deep valley with a mountain opposite it. Is is possible to find a path from the point 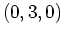 to
to 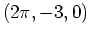 such that the value of
such that the value of 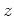 is always between
is always between 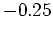 and
and 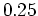 ? You do not have to find a formula for your path, but you must present convincing evidence that it exists. For example, you might want to sketch your path in by hand on an appropriate countour plot. You need to show at least 6 contours in your plot.
? You do not have to find a formula for your path, but you must present convincing evidence that it exists. For example, you might want to sketch your path in by hand on an appropriate countour plot. You need to show at least 6 contours in your plot.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina Solitro
2008-03-19
![]() over a domain, e.g. a set of points in the
over a domain, e.g. a set of points in the ![]() plane. The domain can have any shape, but a rectangular one is the easiest to deal with.
plane. The domain can have any shape, but a rectangular one is the easiest to deal with.
![]() , where
, where ![]() is a constant. In this case, we say the surface is defined implicitly. A third way of representing a surface
is a constant. In this case, we say the surface is defined implicitly. A third way of representing a surface ![]() is through the use of level curves. The idea is that a plane
is through the use of level curves. The idea is that a plane ![]() intersects the
surface in a curve. The projection of this curve on the
intersects the
surface in a curve. The projection of this curve on the ![]() plane is called a level curve. A collection of such curves for different values of
plane is called a level curve. A collection of such curves for different values of ![]() is a representation of the surface called a contour plot.
is a representation of the surface called a contour plot.
![]() plane by letting
plane by letting ![]() be constant, but also in the
be constant, but also in the ![]() plane by holding
plane by holding ![]() constant and the
constant and the ![]() plane by holding
plane by holding ![]() constant.
constant.
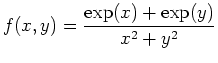 for the
for the 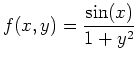 for
for