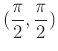Next: About this document ...
Up: lab_template
Previous: lab_template
Subsections
The purpose of this lab is to acquaint you with applications using Maple to compute partial derivatives.
To assist you, there is a worksheet associated with this lab. You can copy that worksheet to your home directory by copying the directory location below to your computer's Start menu search or in your Maple screen, go to File - Open, then paste the dirctory location in the dialogue box where it says file name.
\\storage.wpi.edu\academics\math\calclab\MA1024\Pardiff_tanplane_start_D19.mw
When differentiating a function
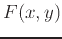 of two (or more) variables, you need to specify which independent variable is being derived.
of two (or more) variables, you need to specify which independent variable is being derived.
A differentiable function,
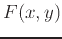 , of two variables has two first order partial derivatives:
, of two variables has two first order partial derivatives:
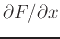 and
and
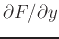 . As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
. As you have learned in class, computing partial derivatives is
very much like computing regular derivatives. The main difference is
that when you are computing
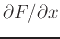 , you must treat
the variable
, you must treat
the variable 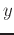 as if it was a constant and vice-versa when computing
as if it was a constant and vice-versa when computing
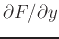 .
.
The Maple commands for computing partial derivatives are D
and diff. The diff command can be used on both expressions and functions whereas the D command can be used only on functions. The commands below show examples of first order and second order partials in Maple.
> f := (x,y) -> x^2*y^2-x*y;
> diff(f(x,y),x);
> diff(f(x,y),y,y);
> D[1](f)(x,y);
> D[2,2](f)(x,y);
Note in the above D command that the 1 in the square brackets means x and the 2 means y.
The next example shows how to evaluate the mixed partial derivative of the function given above at the point
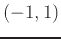 .
.
> eval(diff(f(x,y),x,y),{x=-1,y=1});
> D[1,2](f)(-1,1);
The tangent plane like the tangent line to a single variable function is based on derivatives, however the partial derivatives are used for the tangent plane. Let's start with the equation of the tangent line to the function
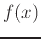 at the point where
at the point where
 . Recall, the general equation of a line at the point
. Recall, the general equation of a line at the point
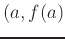 having slope
having slope
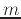 is
is
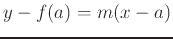 . This can be rewritten knowing that the derivative is the slope of a tangent line as
. This can be rewritten knowing that the derivative is the slope of a tangent line as
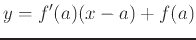 . Similarly for a funcion of two variables, the equation of the plane tangent to
. Similarly for a funcion of two variables, the equation of the plane tangent to 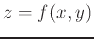 at the point
at the point 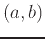 has the equation
has the equation
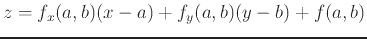 . The following examples will show you how to find the tangent plane to the function
. The following examples will show you how to find the tangent plane to the function
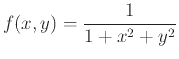 at
at
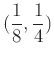 . You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff, the eval or subs command would be used.
. You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff, the eval or subs command would be used.
> f:=(x,y)->1/(1+x^2+y^2);
> tp:=D[1](f)(1/8,1/4)*(x-1/8)+D[2](f)(1/8,1/4)*(y-1/4)+f(1/8,1/4);
> plot3d({f(x,y),tp},x=-1..1,y=-1..1);
To find a point,
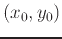 , where the tangent plane is horizontal, you would need to solve where both first order partials are equal to zero simultaneously.
, where the tangent plane is horizontal, you would need to solve where both first order partials are equal to zero simultaneously.
> solve({diff(f(x,y),x)=0,diff(f(x,y),y)=0},{x,y});
The horizontal plane at that point would simply be
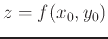 . Since the solve command above yields the
. Since the solve command above yields the 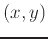 ordered pair
ordered pair 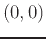 , below is how to plot the surface and the horizontal tangent plane.
, below is how to plot the surface and the horizontal tangent plane.
> tp:=f(0,0);
> plot3d({f(x,y),tp},x=-1..1,y=-1..1);
If 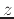 is not explicitly solved for but assumed to be a function of
is not explicitly solved for but assumed to be a function of
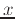 and
and
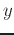 , then the equation can be defined implicitly. Note the difference in the syntax for defining the surface for the implicitplot command. An equal sign must be included in the equation and defined as an expression, not a function. This gives the flexibility of being able to graph equations without having to solve for
, then the equation can be defined implicitly. Note the difference in the syntax for defining the surface for the implicitplot command. An equal sign must be included in the equation and defined as an expression, not a function. This gives the flexibility of being able to graph equations without having to solve for
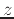 first.
first.
>with(plots):
>surf:=x^2+y^2+z^2=1;
>implicitplot3d(surf,x=-2..2,y=-2..2,z=-2..2);
The tangent plane to an implicitly defined surface
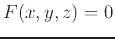 is given below:
is given below:
To find the tangent plane to the sphere
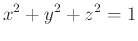 at the point
at the point
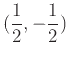 and
and
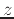 is positive, you would first need to find the coordinating
is positive, you would first need to find the coordinating
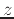 value for the
value for the
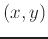 ordered pair. Below is how you would do this in Maple as well as find and plot the tangent plane implicitly.
ordered pair. Below is how you would do this in Maple as well as find and plot the tangent plane implicitly.
>with(plots):
>F:=x^2+y^2+z^2-1;
>solve(eval(F,{x=1/2,y=-1/2}),z);
>a:=eval(diff(F,x),{x=1/2,y=-1/2,z=sqrt(2)/2});
>b:=eval(diff(F,y),{x=1/2,y=-1/2,z=sqrt(2)/2});
>c:=eval(diff(F,z),{x=1/2,y=-1/2,z=sqrt(2)/2});
>tp:=a*(x-1/2)+b*(y+1/2)+c*(z-sqrt(2)/2)=0;
>implicitplot3d({F=0,tp},x=-2..2,y=-2..2,z=-2..2,numpoints=2000);
- Given
- a)
- Find the equation of the plane tangent to the surface
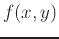 at
at
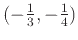 . Plot the surface and the tangent plane on the same graph over the intervals
. Plot the surface and the tangent plane on the same graph over the intervals
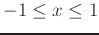 ,
,
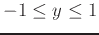 and rotate to see point of tangency.
and rotate to see point of tangency.
- b)
- Find all points on the graph of
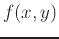 where the tangent plane is horizontal, then find the equation of each horizontal plane and plot them on the same graph as the function
where the tangent plane is horizontal, then find the equation of each horizontal plane and plot them on the same graph as the function 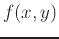 . Use plotting ranges
. Use plotting ranges
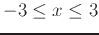 ,
,
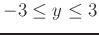 .
.
- a)
- Use implicit methods to find the plane(s) tangent to the ellipsoid
at the point 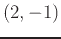 . Plot the tangent plane(s) on the same graph as the ellipsoid and rotate to see the point of tangency. Use plotting ranges
. Plot the tangent plane(s) on the same graph as the ellipsoid and rotate to see the point of tangency. Use plotting ranges
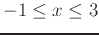 ,
,
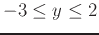 , and
, and
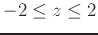 .
.
- b)
- Find all points on the ellipsoid where the tangent plane is horizontal, then find the equation of each horizontal plane and plot them on the same graph using the same plotting ranges given in part a.
- Define the total differential from the linearization of
and estimate the change in u given small changes in 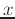 and
and 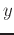 of
of 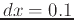 and
and 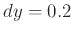 respectively at each of the following points:
respectively at each of the following points:
- a)
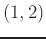
- b)
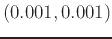
- c)
-
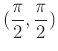
Compare these answers to the actual total differential and explain these results in terms of the fieldplot of 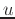 over the intervals
over the intervals
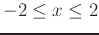 ,
,
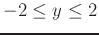 .
.



Next: About this document ...
Up: lab_template
Previous: lab_template
Dina J. Solitro-Rassias
2019-04-04
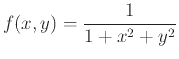 at
at
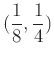 . You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff, the eval or subs command would be used.
. You could write the partials with diff or D. This example uses D as it is easier to plug in the the point with this syntax; with diff, the eval or subs command would be used.
![]() , where the tangent plane is horizontal, you would need to solve where both first order partials are equal to zero simultaneously.
, where the tangent plane is horizontal, you would need to solve where both first order partials are equal to zero simultaneously.
![]() . Since the solve command above yields the
. Since the solve command above yields the ![]() ordered pair
ordered pair ![]() , below is how to plot the surface and the horizontal tangent plane.
, below is how to plot the surface and the horizontal tangent plane.
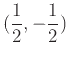 and
and