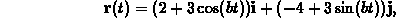
where b is a positive constant.
- Show that the trajectory, or image curve, of
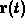 is the
circle of radius 3 centered at the point
is the
circle of radius 3 centered at the point 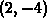 . That is, show
that the component functions
. That is, show
that the component functions 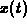 and
and 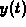 of
of 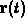 satisfy
the equation
satisfy
the equation
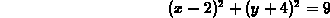
for all values of t. Explain why this means that the image curve is the circle in question.
- Show that the speed is constant and explain why this is so. Then find a value of the constant b that gives a speed of 18.
- Show that
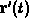 is perpendicular to
is perpendicular to 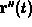 .
.
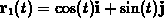 . Particle 2,
on the other hand, is going back and forth on the line y=ax with
position function
. Particle 2,
on the other hand, is going back and forth on the line y=ax with
position function 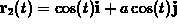 ,
where a is a constant.
,
where a is a constant.
- If a=3, find the value of t,
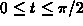 , for
which the two particles collide.
, for
which the two particles collide.
- Is it possible to find a positive real number a for which the
two particles do not collide for any value of t,
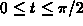 ? Explain your answer.
? Explain your answer.
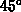 angle. Find
the angle
angle. Find
the angle 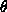 , measured from the horizontal, that the projectile
should be fired at to maximize the distance, measured along the hill,
the projectile travels before it hits the hill.
, measured from the horizontal, that the projectile
should be fired at to maximize the distance, measured along the hill,
the projectile travels before it hits the hill.