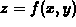In this lab we will consider the case of a surface defined explicitly
by an equation of the form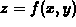 
. Generalizations may be
introduced in subsequent labs and/or classes.
One problem that comes up again and again in engineering and science is how to graphically represent functional relationships between more than two variables. The basic problem is one of trying to represent objects in three (or more) dimensions as two-dimensional plots. You have already had experience with Maple's plot3d command, which allows you to view a two-dimensional representation of a surface in three dimensions from various angles. This is not the only representation method, however. Another extremely useful method involves plotting what are known as the contours.
Suppose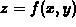 
is the equation of a surface in three dimensions
and C is a
constant. The solution of the equation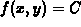 
can be visualized
graphically by plotting the function together with the plane z=C.
The curve generated by this intersection is often referred to as a
contour. Note that this curve lies on the surface.
For example, the intersection of the two surfaces displayed by the
maple command
> plot3d({x^2+y^2,4},x=-3..3,y=-3..3);
would be the solution of the equation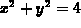 
.
There are several cases where it is important to be able to find the
curves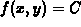 
as the parameter C is varied, including the
following.
In fact, drawing the contours of a function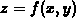 
in the xy
plane is another way of representing a surface in two dimensions. That
is, given the contour lines you should be able to reconstruct the
surface and vice-versa. There are several ways you can get Maple to
generate the contours on a plot generated with the plot3d
command. One way is with the style=CONTOUR option, as in the
following example.
> plot3d(x^2+y^2,x=-2..2,y=-2..2,style=CONTOUR);
However, it is probably easier to generate the contours after you have used plot3d to render the surface by using the Contours and Patch and Contour options in the Style menu in the Maple 3D plotting window. One thing to note is that Maple plots the contours right on the surface. Usually, by a contour plot one means the projection of the contour curves onto the x-y plane. To see this in Maple, just view the plot from above or below, that is, along the z axis.
Contours on a surface are just one example of curves on a
surface. Another important example is what is known as a
trace
of a surface. Geometrically, a trace is the intersection of a
plane x=a or y=b, where a and b are constants, with a surface
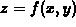. For example, the intersection of the plane x=1 with our
example surface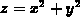 
can be described by the equations
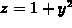, x=1. This trace can be plotted in at least two ways. We
could just plot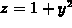 
in the yz plane, as in the following
command.
> plot(1+y^2,y=-2..2);
Another way would be to
plot the curve x=1,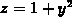 
in three dimensions. Even better would
be to plot the trace right on the surface. This turns out not to be as
simple as one would like, so a Maple procedure SurfLoop has been
written that does the job. It is part of the CalcP package, so
you have to load the package first. Once you've done that, the command
to display the surface and the trace in the same plot is the
following.
> SurfLoop(x^2+y^2,x=-2..2,y=-2..2,[1,t],t=-2..2);
The trace curve should appear in green.
The syntax of the SurfLoop command needs a little
explanation. The first three arguments are exactly the same as for a
plot3d command for plotting the surface. The next two arguments
give a parametric curve in the xy plane and a range for the variable
t. The way SurfLoop works is that it projects this parametric
curve onto the surface. That is, if the parametric curve is given by
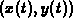and the surface is given by 
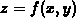the SurfLoop
command plots the three-dimensional parametric curve
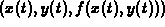. In the example, we wanted the trace for
x=1, so an easy choice for the parametric curve was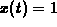 
, 
.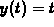