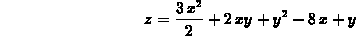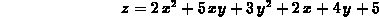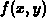Exercises

1. Generate the contours for the following functions and describe what you see.
   1. .
   2. .
   3. .
   4. .
   5. .
   6. .
2. The contours are generated at equally-spaced values of z. Can you relate the distance between the contours in a two-dimensional contour plot to rates of change of the function?
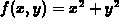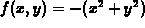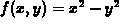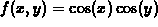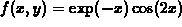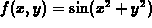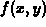3. Can you distinguish between the two-dimensional contour plots of and 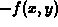? If so, how? If not, how would you overcome this problem?
4. Describe how Maple uses traces to generate surfaces plotted with the Wireframe style in the plot3d command.
5. Suppose that you have a function of the form

   

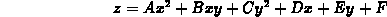
   where A - F are constants and, furthermore, A is positive. Then it is a general result that the graph of such a function is similar to the graph of exactly one of the following two functions, both of which appeared in the first exercise.

   

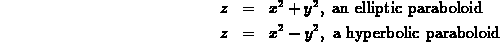
   For the following functions, determine whether they are elliptic paraboloids or hyperbolic paraboloids. Your explanation should be in terms of contours and/or traces.

   1. 

   2. 

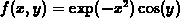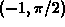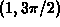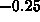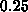6. Consider the function , which looks like a deep valley with mountains on either side. Can you find a curve in the xy plane between the points and such that its projection onto this surface has z coordinate always between and ? (Hint - it might be helpful to use the view argument to the plot3d command. See the help for plot3d[options] for details.)