Exercises

1. Give a vector valued function whose graphical representation is a helix of radius 3 and whose axis is the vertical straight line passing through the point (0,2,0). Plot the helix and make a reference to it in your writeup.
2. Using only Maple, do problems 14, 16, and 18 from section 11.2 of the text.
3. Consider the two-dimensional position vector

   

   where b is a positive constant.

   1. Determine the trajectory curve of 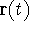. Be specific.(i.e. An ellipse centered at the origin intersecting its major axis at (-5,0) and (5,0) and intersecting its minor axis at (0,3) and (0,-3)). Be sure to explain how you determined the trajectory curve from the given position vector.
   2. Show that the speed is constant and explain why this is so. Then find a value of the constant b that gives a speed of 18.
   3. Show that 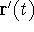is perpendicular to .
4. Suppose particle 1 is going around a circle and its position is given by . Particle 2, on the other hand, is going back and forth on the line y=ax with position function , where a is a constant.
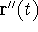   1. If a=4, find the value of t, 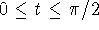, for which the two particles collide.
   2. Is it possible to find a positive real number a for which the two particles do not collide for any value of t, 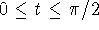? Explain your answer.