Subsections

• Purpose
• Structure
• Problem 1: Finding Extrema
  • Background
  • Example
  • Exercise
• Problem 2: Extrema in Economic Modeling
  • Background
  • Example
  • Exercise
• Problem 3: Modeling Data
  • Background
  • Example
  • Exercise

Applications of Extrema of Functions of Two Variables

Purpose

The purpose of this lab is to give you experience in applying calculus techniques relating to finding extrema of functions of two variables.

Structure

There are three problems, each of which has a background discussion, an illustrative example, and an exercise for you to do. Most of the basic theoretical background you will need has been covered in Lab 3, but there will be a little repetition here for completeness. Most of the Maple procedures you will need have been covered in previous labs, but there will be a few new ones introduced below.

Problem 1: Finding Extrema

Background

For some simple functions of two variables, it is not difficult to determine their relative extrema by first finding the critical points and then applying the Second Partials Test (SPT) to discriminate among relative maxima, relative minima, and saddle points. Recall that if the function f(x,y) is differentiable, then (x₀,y₀) is a critical point if ${\nabla f}(x_0,y_0)=0$. With D=f_xx(x₀,y₀)f_yy(x₀,y₀)-[f_xy(x₀,y₀)]², the SPT is as follows:

		 If D>0 and fxx(x0,y0)>0, then f has a relative minimum at (x0, y0).
		 If D>0 and fxx(x0,y0)<0, then f has a relative maximum at (x0, y0).
		 If D<0, then  (x0, y0) is a saddle point of f.
		 If D=0, then the test is inconclusive. 

Many applications described by functions of two variables can be studied by purely analytical means, but computer software such as Maple might be of substantial help in gaining further insight or obtaining information that cannot be found analytically. In Lab 3, you used Maple tools such as diff, solve, fsolve for finding critical points and extrema and applying the SPT. In this lab, we will encourage the use of more powerful Maple tools, such as the grad command mentioned in Lab 3, in combination with tools for visualization such as plot and plot3d.

Example

To find the relative extrema of f(x,y) = -x³ + 4xy - 2y² + 1, first find the critical points by determining where f_x(x,y)=f_y(x,y)=0. Solving these equations analytically leads to the two critical points (0,0) and (4/3,4/3). Applying the SPT to the critical points, you find that (0,0) corresponds to a saddle point of f, whereas f has a relative maximum at (4/3,4/3).

The following commands carry out the solution procedure in Maple:

  > f:=(x,y)->-x^3+4*x*y-2*y^2+1;

  > with(linalg);

  > gradf:=(x,y)->grad(f(x,y),[x,y]);

  > solve({gradf(x,y)[1]=0,gradf(x,y)[2]=0},{x,y});

If you want to see what ${\nabla f}(x,y)$ is, you can type

  > gradf(x,y);

Having used Maple to solve the problem analytically, you can also use it to view the f-surface with plot3d, e.g.,

  > plot3d(f,-40..40,-40..40,grid=[40,40],axes=boxed);

You can use the mouse to adjust the angle of view and get a lot of insight into what the f-surface looks like. However, for this surface, it would be very difficult to determine the critical points by visual inspection; analytical tools are still necessary.

Exercise

An army company works in the field with subsurface radar to detect small antipersonnel mines that are restricted by an international convention. An active element of the radar is a rectangular planar antenna array that is used to explore an area of ground (the xy-plane) to determine an informative signal S=f(x,y). In the absence of mines, the radar gets no informative signal and S=f(x,y)=0. If mines are present, the signal function S has a maximum at those points (x₀,y₀) that specify the xy-coordinates of the geometric centers of the mines.

Suppose the array has been applied to a suspected area of the ground, and the radar receives a signal which, after appropriate electronic manipulation of the signal-to-noise ratio, is represented by
S = (x² + 4y²)e^(1-x2-y2), where x and y are rectangular coordinates of the area covered by the array (in units of meters). How many mines are found by this application? What is the distance between the mines, i.e., between their centers?

Problem 2: Extrema in Economic Modeling

Background

Extrema of functions of several variables are important in numerous applications in economics and business. Particularly important variables are profit, revenue, and cost. Their rates of change (i.e., derivatives) with respect to the number of units produced or sold are referred to as marginal profit, revenue, and cost. These are central to many applications involving extrema. For instance, to find the maximum profit, the profit function, P=R-C, is analyzed. In the formula, R=xp is the total revenue from selling x units, where p is the price per unit, and C is the total cost of producing x units. The differentiation of the profit function is carried out with respect to x. Assuming the result of the differentiation is equal to zero, one can see that the maximum profit occurs when the marginal revenue (that is, dR/dx) is equal to the marginal cost (that is, dC/dx).

Practical profit problems usually involve several models of one type of product, with prices per unit and profits per unit varying from model to model, and demand for each model which is a function of the price of the other models as well as its own price, etc.

Example

The profit obtained by producing x units of product A and y units of product B is approximated by the model

P(x,y) = 8x + 10y - (0.001)(x² + xy + y²) - 10,000.

To find the production level that produces a maximum profit, the partial derivatives of the profit function are set equal to 0, and the resulting system of two equations is solved with respect to x and y; this gives x=2,000 and y=4,000. The SPT shows that P_xx<0 and P_xxP_yy-P_xy²>0, which means the obtained production level (x = 2,000 units, y = 4,000 units) indeed yields a maximum profit. The solution procedure using Maple is similar to that in Problem 1.

Exercise

1

To reduce shipping distances between the manufacturing facilities and a major consumer, a Korean computer brand, Intel Corp. intends to start production of a new controlling chip for Pentium III microprocessors at their two Asian plants. The cost of producing x₁ chips at Chiangmai (Thailand) is

C₁ = 0.002x₁² + 4x₁ + 500,

and the cost of producing x₂ chips at Kuala-Lumpur (Malaysia) is

C₂ = 0.005x₂² + 4x₂ + 275.

The Korean computer manufacturer buys them for $150 per chip. Find the quantity that should be produced at each Asian location to maximize the profit if, in accordance with Intel's marketing department, it is described by the expression:

P(x₁, x₂) = 150(x₁ + x₂) - C₁ - C₂.

Get the answer first by analytical means and then confirm it by visualizing the function P(x,y) and determining the extremal value.

2

Repeat the same process as in part a, however, this time we are going to use numbers which are a bit more realistic. We also know that the maximum number of chips that the second plant can ship to the manufacturing plant in Korea is 11,000 chips.

C₁ = 0.001998x₁² + 3.813x₁ + 531.6

C₂ = 0.005698x₂² + 4.045x₂ + 349.6

P(x₁, x₂) = 148.6(x₁ + x₂) - C₁ - C₂

Problem 3: Modeling Data

Background

Many applications involve mathematical models that describe a phenomenon of interest. Often these models are based on some mathematical form. For example, a dependent variable y might be modeled by a function y=f(x) of a certain type, which could be a straight line, a higher order polynomial, an exponential function, or some other specified type of function. In constructing a model to represent a particular phenomenon, the goals are simplicity and accuracy. These goals conflict quite often in choosing a type of function to be used in a model.

Often function types used in models involve parameters that are determined so that the model function ``fits'' observed data in an optimal way. An especially popular way to specify parameters to ``fit'' data is the Method of Least Squares. In this, if y = f(x) is the model function and $\{(x_1,y_1),...,(x_n,y_n)\}$ is a set of observed data, then the measure of ``goodness of fit'' is the sum of squared residuals

$$S = \sum_{i=1}^n[f(x_i) - y_i]^2.$$

Graphically, S can be interpreted as the sum of the squares of the vertical distances between the graph of f and the given points in the plane. The smaller S is, the better the fit. If the model is perfect, then S = 0. Most likely, it is not, so you settle for a choice of parameters that minimizes S.

Perhaps the simplest model function is a linear model y=f(x)=mx+b. In this case,

$$S=\sum_{i=1}^n[mx_i+b - y_i]^2.$$

With m and b chosen to minimize this S, the resulting linear model is called the least squares regression (LSR) line. It is easy to see (and shown in the text on p. 801) that S has exactly one critical point, given by

$$m={{n\sum_{i=1}^nx_iy_i-\left(\sum_{i=1}^nx_i\right) \left(\... ...)}\over{ n\sum_{i=1}^nx_i^2-\left(\sum_{i=1}^nx_i\right)^2}}\;,$$

and this m and b minimize S.

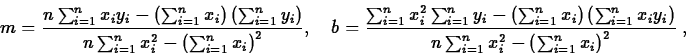
Remarks: Historically, the Method of Least Squares has been popular because it is often (if not always) easy to implement, often (if not always) gives satisfactory results, and has especially appealing interpretations in some contexts, notably regression and maximum-likelihood estimation in statistics. One can show that if the parameters that determine a model function appear linearly in the function, as in the linear and quadratic models above, then, as above, the parameters that minimize the sum of squared residuals can be obtained by solving a certain linear system, which is usually a relatively easy task. There is often a temptation with least squares modeling to go to increasingly complicated model functions in order to get increasingly better fits, as measured by the sum of squared residuals. For example, a quadratic model will give a smaller sum of squared residuals than a linear model, a cubic model will give a still smaller sum of squared residuals, and so on. However, in addition to increasing model complexity, this sort of thing may lead to subtle dangers, e.g., numerical methods for solving the linear systems may become inaccurate. In particular, if the model is to be used for extrapolation, i.e., prediction beyond the range of observed data values, then more complicated models are often far less reliable than simpler ones.

Example

Assume there are five data points $\{(0,1),(1,3),(2,2),(3,4),(4,5)\}$, and suppose we want to find the LSR line. Forming and solving the above equations for m and b, one obtains m=0.9 and b=1.2, and the LSR line is y=0.9x+1.2.

Using Maple, one can carry out the solution procedure based on the above equations in a straightforward way.

First we must enter the data in convenient arrays ...

  > xdata:=[0,1,2,3,4];

  > ydata:=[1,3,2,4,5];

Now create the function that is the LSR line ...

  > resid := (a,b) -> sum((ydata[i]-(a*xdata[i]+b))^2,i=1..5);

  > coefficient := solve({diff(resid(a,b),a)=0,diff(resid(a,b),b) =0},{a,b});

  > lfun := x -> subs(coefficient,a*x + b);

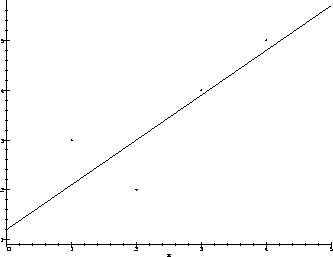
Finally, we will graph the (x,y)-data together with the LSR line. First load the (x,y)-data in suitable form

  > data:=[[xdata[n],ydata[n]] $n=1..5];

Now plot the data together with the LSR line (the following looks a lot better on a screen) ...

> plot([data,lfun(x)],x=0..5,color=[red,blue],style=[point,line]);

Remark: Don't forget to use Maple help to see much more about these commands and many more possibilities for customizing plots, etc.

Exercise

Wolfgang Amadeus Mozart (1756-1791) was one of the most prolific composers of all time. In 1862, the German musicologist Ludwig von Köchel made a chronological list of Mozart's musical work. This list is the source of the Köchel numbers, or "K numbers", that now accompany the titles of Mozart's pieces (e.g., Sinfonia Concertante in E-flat major, K. 364). The table below gives the Köchel numbers and composition dates of 10 of Mozart's works.

Köchel Number Year Composed

1 1761

75 1771

155 1772

219 1775

271 1777

351 1780

425 1783

503 1786

575 1789

626 1791

In this exercise, do the following:

(a)

Plot the year y versus the Köchel number K.

(b)

Find the Least Squares Regression Line y = mK + b for the data. Compare the line with the plot drawn in (a). What is difference?

(c)

K. 364 was actually composed in 1779. What date is predicted by the LSR line?

(d)

If Mozart had lived, when would he have finished his next 100 works, i.e., in what year would he have finished K. 726? Compare answers given by the LSR line.