


Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Subsections
The purpose of this lab is to give you practice using Maple to plot vector
valued functions and their derivatives.
Maple procedures are available to study vectors and vector-valued functions.
This lab will introduce commands that we
have written here at WPI as part of the CalcP package. Before you can
use any of these commands, you must load them using the with command.
Since some of the commands use the linalg
package, it is probably a good idea to load it as well.
> with(linalg):
Warning: new definition for norm
Warning: new definition for trace
> with(CalcP):
The
list below gives the names of the procedures we will be using, as well
as brief descriptions. Maple help screens are available for all
of these procedures, so refer to them for further examples. To refresh
your memories, the commands introduced in the previous lab are also
listed.
- VDiff
- Differentiates vector-valued functions.
- VPlot
- Plots vector-valued functions in two and three
dimensions.
- VMag
- Computes the magnitude of a vector.
- ParamPlot
- Animates parametric curves in two dimensions.
- ParamPlot3D
- Animates parametric curves in three dimensions.
- Speed
- Computes the speed of a particle moving on a path defined
by a vector-valued function
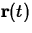 .
. - unitvect
- Computes the unit vector associated with a vector
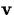 .
. - tanvect
- Computes the unit tangent vector,
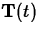 , for a
vector-valued function
, for a
vector-valued function 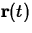 .
.
For more examples, see the help screens for the individual procedures.
Note that all of the procedures
accept either Maple vectors or Maple lists as arguments. Note also
that several of the procedures allow you to evaluate the result at a
specific value of t by using a second argument of the form
t=a (to evaluate at t=a). If the second argument is simply
t, then the result of the procedure is an expression involving
t. This does not apply to the VDiff command, however, where
argumets after the first are used to indicate derivatives.
> circ := t -> vector([12*sin(t),12*cos(t)]);
![\begin{maplelatex}
\begin{displaymath}
{\it circ} := {t} \rightarrow {\rm vector...
...rm sin}(\,{
t}\,), 12\,{\rm cos}(\,{t}\,)\,]\,)\end{displaymath}\end{maplelatex}](img4.gif)
> VDiff(circ(t),t);
![\begin{maplelatex}
\begin{displaymath}[\,12\,{\rm cos}(\,{t}\,)\, - 12\,{\rm sin}(\,{t}\,)\,]\end{displaymath}\end{maplelatex}](img5.gif)
> r := t -> vector([t,t^2]);
![\begin{maplelatex}
\begin{displaymath}
{r} := {t} \rightarrow {\rm vector}(\,[\,{t}, {t}^{2}\,]\,)\end{displaymath}\end{maplelatex}](img6.gif)
> tanvect(r(t),t);
![\begin{maplelatex}
\begin{displaymath}
\left[ \! \,{\displaystyle \frac {1}{\sq...
...+ 4\,{t}^{2}\, \! \right\vert }}}\, \! \right] \end{displaymath}\end{maplelatex}](img7.gif)
> tanvect(r(t),t=1);
![\begin{maplelatex}
\begin{displaymath}
\left[ \! \,{\displaystyle \frac {1}{5}}...
...laystyle \frac {2}{5}}\,\sqrt {5}\, \! \right] \end{displaymath}\end{maplelatex}](img8.gif)
The next few commands deal with a simple example of a curve known as a
helix. In one of the exercises, you will be asked to generate a curve similar
to a helix. If we want to visualize the projection of a helix onto the x,y-plane, we can rotate the plot of the graph, so that the z axis, would be perpendicular to the computer monitor. In other words the the z component would be pointing in/out of the screen. Notice in this case the projection of the the helix onto the x,y-plane would be a circle.
> h := t -> vector([cos(t),sin(t),t]);
![\begin{maplelatex}
\begin{displaymath}
{h} := {t} \rightarrow {\rm vector}(\,[\,{\rm cos}(\,{t}\,),
{\rm sin}(\,{t}\,), {t}\,]\,)\end{displaymath}\end{maplelatex}](img9.gif)
> VPlot(h(t),t=0..4*Pi);
> ParamPlot3D(h(t),t=0..4*Pi);
> Speed(h(t),t);
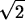
- 1.
- Find a vector-valued function
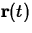 whose graph lies on the cone
x2+y2=2z, such that the graph spirals around the cone and the
whose graph lies on the cone
x2+y2=2z, such that the graph spirals around the cone and the 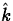 component is increasing. (You can think of this as motion of a particle spiraling around the cone)
component is increasing. (You can think of this as motion of a particle spiraling around the cone)
- (a)
- Plot the graph of your function.
- (b)
- Find the derivative of your function and plot the graph of this derivative.
- (c)
- Find and plot the magnitude of this derivative (which is Speed).
- (d)
- If the speed is not a decreasing function, figure
out a way to change your original function so that the speed is a decreasing
function of t. Plot the speed for the new function to demonstrate
that it is decreasing.
- 2.
- Find a vector-valued function
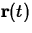 such that the projection of
its graph onto the
x,y-plane is a circle of radius 1 and the projection onto the y,z-plane
is a circle of radius, 1 both of which are centered at the origin.
such that the projection of
its graph onto the
x,y-plane is a circle of radius 1 and the projection onto the y,z-plane
is a circle of radius, 1 both of which are centered at the origin.
- (a)
- Plot the graph of your function.
- (b)
- Plot the projections onto the x,y and y,z-planes.
- (c)
- Plot the projection onto the x,z-plane. Is it possible to have this
projection be a circle too? Why? In fact, what can you say must be true about
this projection, if the others are the circles we specified?
- 3.
- Find a vector-valued function
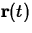 that is equal to its
derivative. Hint: think about what scalar function has the property that its derivative is itself.
that is equal to its
derivative. Hint: think about what scalar function has the property that its derivative is itself.
- (a)
- Plot
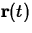 .
.
- (b)
- Plot the second derivative of
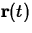 .
.
- (c)
- Can you characterize all vector-valued functions that are equal to their
derivatives? Of what form must they
be?



Next: About this document ...
Up: Labs and Projects for
Previous: Labs and Projects for
Christine M Palmer
3/17/1998
![]()
![]()
![]()
![\begin{maplelatex}
\begin{displaymath}
\left[ \! \,{\displaystyle \frac {1}{\sq...
...+ 4\,{t}^{2}\, \! \right\vert }}}\, \! \right] \end{displaymath}\end{maplelatex}](img7.gif)