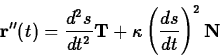Next: About this document ...
Up: No Title
Previous: No Title
Subsections
The purpose of this lab is to introduce you to curve computations
using Maple for parametric curves and vector-valued functions in the
plane.
By parametric curve in the plane, we mean a pair of equations x=f(t)
and y=g(t) for t in some interval I. A vector-valued function in
the plane is a function 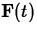 that associates a vector in
the plane with
each value of t in its domain. Such a vector valued function can
always be
written in component form as follows,
that associates a vector in
the plane with
each value of t in its domain. Such a vector valued function can
always be
written in component form as follows,
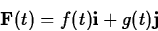
where f and g are functions defined on some interval I. From our
definition of a parametric curve, it should be clear that you can
always associate a
parametric curve with a vector-valued function by just considering the
curve traced out by the head of the vector. However, there are
lots of situations where a vector-valued function is more
appropriate. This happens most often when the quantity you want to
describe with the function is natural to think of as a vector, for
example, a force or a displacement. However, there can be situations when
the quantity is not a vector, but it is convenient to think of it as a
vector to simplify the notation or the calculations. The idea to keep
in your mind is that one of the motivations of vector notation is to
simplify and clarify calculations or other manipulations.
Many applications of calculus to engineering or science involve
parametric curves or vector valued functions, including the examples
listed below.
- The kinematics of mechanisms, like internal combustion engines.
- Population models involving more than one species.
- Chemical kinetics in systems with more than one chemical
species.
- Forced or transient responses of electrical circuits.
For the applications we will deal with, we only need to consider
curvilinear motion of a point in the plane, That is, we have a
vector-valued function 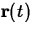 that gives the position at time
t of a moving point P in the plane. The velocity of this point is
given by the derivative
that gives the position at time
t of a moving point P in the plane. The velocity of this point is
given by the derivative 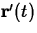 and the acceleration is given
by the second derivative,
and the acceleration is given
by the second derivative, 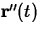 . If the velocity,
. If the velocity,
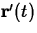 , is not the zero vector, then it is clear from the
way it is defined that
, is not the zero vector, then it is clear from the
way it is defined that 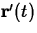 is a vector that is tangent to
the curve at the point
is a vector that is tangent to
the curve at the point 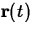 . A simple example of
curvilinear motion is when the velocity is constant. That is, there is
a fixed vector
. A simple example of
curvilinear motion is when the velocity is constant. That is, there is
a fixed vector 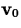 such that
such that
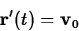
In this case, the motion is along a straight line, with
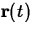 given by
given by
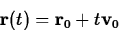
where 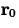 is the position at t=0.
is the position at t=0.
In many applications of
curvilinear motion, we need to know the magnitude of the velocity, or
the speed. This is easy to compute - just take the magnitude 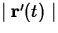 . If f and g are the component functions of
. If f and g are the component functions of
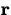 , then the speed is given by
, then the speed is given by
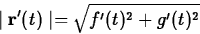
Using our idea of the parametric curve associated with
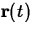 and recalling the definition of arc length, we arrive
at a different interpretation of speed as the rate of change of
arc length, or
and recalling the definition of arc length, we arrive
at a different interpretation of speed as the rate of change of
arc length, or
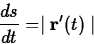
where s is arc length.
This should make sense, if you recall that speed is the rate of change
of distance with time and arc length is distance measured along a
curve.
If the speed is not zero for any value of t in the interval I,
then it is possible to define a unit vector, 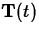 that is
tangent to the curve as follows.
that is
tangent to the curve as follows.
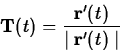
Using this definition, you can write the velocity in the following form.
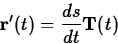
Now, it is natural for the student to ask why one would want to do
this. Computing the velocity using the right hand side of the equation
above is certainly more difficult than taking the derivative of
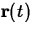 , so this equation is not really useful from a
computational viewpoint. The answer to this is that the unit tangent
vector T at a particular point on the curve is an intrinsic property
of the curve, at least up to a sign change. To use an analogy, think of the
curve as being a one-way road. Different drivers can drive at different
speeds, but at a particular point on the road, each car is
pointed in the same direction, i.e. the direction of the unit tangent
vector at that point. Now suppose that the road allows traffic in
both directions. If you think about it a little, it should be clear
that if the tangent vector at a particular point on the road for
traffic going one direction is
, so this equation is not really useful from a
computational viewpoint. The answer to this is that the unit tangent
vector T at a particular point on the curve is an intrinsic property
of the curve, at least up to a sign change. To use an analogy, think of the
curve as being a one-way road. Different drivers can drive at different
speeds, but at a particular point on the road, each car is
pointed in the same direction, i.e. the direction of the unit tangent
vector at that point. Now suppose that the road allows traffic in
both directions. If you think about it a little, it should be clear
that if the tangent vector at a particular point on the road for
traffic going one direction is 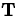 , then the tangent vector at the
same point for traffic going the opposite direction is
, then the tangent vector at the
same point for traffic going the opposite direction is 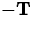 .
.
Now suppose, to carry our analogy a little further, that you wanted to
analyze the acceleration of a car as it traversed the road. On
sections where the road is straight, acceleration depends only on
whether the car is speeding up or slowing down. In a curve, however,
there is an additional acceleration, called the centripetal
acceleration, that is needed to keep the car on the road. The
magnitude of this acceleration depends on the speed of the car and the
sharpness of the curve. It turns out that you can quantify the
sharpness of a curve with an intrinsic property of the curve called
the curvature, usually denoted 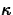 , defined by the following
equation.
, defined by the following
equation.
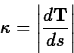
That is, the curvature is the magnitude of the rate of change of the
tangent vector 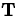 with respect to arc length. For example,
the curvature of a straight line is zero and it can be shown that the
curvature of a circle of radius R is the same for every point on the
circle and is given by
with respect to arc length. For example,
the curvature of a straight line is zero and it can be shown that the
curvature of a circle of radius R is the same for every point on the
circle and is given by 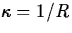 .
.
If the curvature is never zero for a particular curve, then we can
define another intrinsic property of curve, the unit normal vector
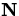 by the following equation.
by the following equation.
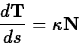
It can be shown that at each point on the curve the vector 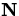 defined
by this equation is a unit vector that is always perpendicular to the
tangent vector T at that point. Furthermore, the unit normal vector
defined
by this equation is a unit vector that is always perpendicular to the
tangent vector T at that point. Furthermore, the unit normal vector
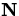 always points in the direction of the centripetal
acceleration required to keep a particle moving on the curve. One way
to see this is to compute the acceleration by differentiating both
sides of the equation
always points in the direction of the centripetal
acceleration required to keep a particle moving on the curve. One way
to see this is to compute the acceleration by differentiating both
sides of the equation
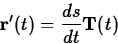
for the velocity and using the chain rule and the definition of the
curvature and the normal vector to obtain the following important
equation.
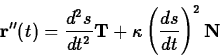
To see why this equation is important, recall that ds/dt is the
speed, so d2s/dt2 is the rate of change of the speed. In our
analogy of a car driving on a road, this term measures whether the car
is speeding up or slowing down. Because this component of the
acceleration is in the direction of the tangent vector it is often
called the tangential acceleration, denoted with the symbol aT. The
component of the acceleration in the direction of the normal vector is
called the normal acceleration, denoted aN.
Computing these intrinsic properties of a curve is generally not an
easy task. The Getting started worksheet for this lab
describes commands from the CalcP package that simplify these
calculations and provides examples for you to work from.
- 1.
- Suppose that at time zero, flight 12 is at the point
(-100 mi,-100 mi) at an altitude of 30,000 feet and traveling
Northeast at 420 mph and that flight 33 is at the same altitude, but
is traveling due west at a speed of 388 mph. At time zero, flight 33
is at the point (200 mi, 30 mi).
- (a)
- What is the minimum distance between flights 12 and 33, and at
what time does it occur?
- (b)
- Suppose that FAA regulations require that the closest approach
of any two aircraft must not be less than 2000 feet. Can you change the
speed of flight 33 so that this regulation is satisfied? What is your
new speed, and what is the closest approach distance?
(Hint - set up parametric descriptions of the positions of the two
flights and use the distance formula. Make sure that you explain each
step of your procedure.)
- 2.
- Consider the curve in the plane given by y=x2 for
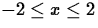 and the two different parametrizations given below. In each
case t is restricted to the interval
and the two different parametrizations given below. In each
case t is restricted to the interval 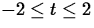 .
.
- (a)
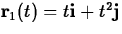
- (b)
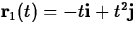
- (a)
- Describe the difference between these two different
parametrizations.
- (b)
- Compute the unit tangent vector
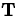 at the point x=0,
y=0 for each parametrization and explain your results.
at the point x=0,
y=0 for each parametrization and explain your results.
- (c)
- Compute the curvature and the unit normal vector at the point
x=0, y=0 for each parametrization and explain your results.
- 3.
- A hairpin turn on a roadway can be approximated as half of an
ellipse, including the half of major (longer) axis. If the major axis is 100
feet and the minor axis is 80 feet, what is the maximum (constant)
speed a car can go through the turn while keeping the centripetal
acceleration less than 0.3g, where g is the acceleration due to
gravity?
- 4.
- Consider
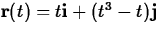 . What is the
normal vector at t=0.01? At t=-0.01? What about at t=0? What
goes wrong?
. What is the
normal vector at t=0.01? At t=-0.01? What about at t=0? What
goes wrong?
- 5.
- For
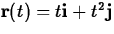 with
with 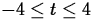 , answer the following questions.
, answer the following questions.
- (a)
- For which value of t is the speed a maximum?
- (b)
- For which value of t is the curvature a maximum?
- (c)
- For which value of t is the tangential acceleration a maximum?
- (d)
- For which value of t is the normal acceleration a maximum?



Next: About this document ...
Up: No Title
Previous: No Title
William W. Farr
3/23/1999
![]()
![]()
![]()
![]()
![]() that gives the position at time
t of a moving point P in the plane. The velocity of this point is
given by the derivative
that gives the position at time
t of a moving point P in the plane. The velocity of this point is
given by the derivative ![]() and the acceleration is given
by the second derivative,
and the acceleration is given
by the second derivative, ![]() . If the velocity,
. If the velocity,
![]() , is not the zero vector, then it is clear from the
way it is defined that
, is not the zero vector, then it is clear from the
way it is defined that ![]() is a vector that is tangent to
the curve at the point
is a vector that is tangent to
the curve at the point ![]() . A simple example of
curvilinear motion is when the velocity is constant. That is, there is
a fixed vector
. A simple example of
curvilinear motion is when the velocity is constant. That is, there is
a fixed vector ![]() such that
such that
![]()
![]()
![]() . If f and g are the component functions of
. If f and g are the component functions of
![]() , then the speed is given by
, then the speed is given by
![]()
![]()
![]() that is
tangent to the curve as follows.
that is
tangent to the curve as follows.
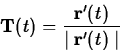
![]()
![]() , defined by the following
equation.
, defined by the following
equation.
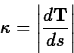
![]() by the following equation.
by the following equation.
![]()
![]()