Midterm Exam given in term B97, November 18, 1997
Post-script version
- 1.
- (20 points) Solve each of the following initial-value problems:
- a.
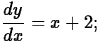 y(2) = 3.
y(2) = 3.
- b.
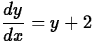 ; y(2) = 3.
; y(2) = 3.
- 2.
- (30 points) Consider the differential equation
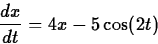
- a.
- Find a nontrivial solution to the homogeneous equation.
- b.
- Find a particular solution to the differential equation
- c.
- Find the general solution to the equation.
- d.
- Consider the solutions with two different initial
values. Do the solutions get farther apart or closer together as t
increases? Justify your answer.
- 3.
- (30 points) Water is being poured into a tank at a constant rate
of 3 liters per second. A small leak at the bottom of the tank causes
water to leak out at a rate proportional to the amount of water in the
tank. Suppose that initially there is 400 liters of water in the tank and
that initially the leaking rate is 4 liters per second.
- a.
- Write an expression for the amount of water that is
added to the tank in a small time period. Write an
expression for the amount of water that leaves the tank
in the same small time period.
Define any variables you use.
- b.
- Write an equation that gives the change in the amount
of water over a small time period. Use this equation
to create a differential equation model for the amount
of water in the tank as a function of time.
- c.
- What is the physical meaning of the free and
forced response of this model?
- 4.
- (25 points)
Consider the differential equation u' = 2 - u + u2.
- a.
- Find the equilibria of this differential equation.
- b.
- Where are solutions to this equation increasing?
Where are they decreasing?
- c.
- Decide whether each equilibrium in part (a) is stable
or unstable.
Nathan Gibson
1/27/1998
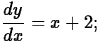 y(2) = 3.
y(2) = 3.
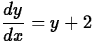 ; y(2) = 3.
; y(2) = 3.
![]()