- (a)
-
The roots for the characteristic equation are -3 and -2 so
two solutions are
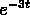and 
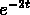. To verify independence,
compute the Wronskian and show that it is not zero.
- (b)
-
Use the method of undetermined coefficients to find
.
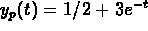- (c)
-
The general solution is
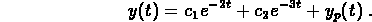
The initial data gives
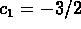and 
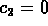so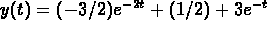 
.
- (d)
-
For large values of t, the solution approaches the constant
solution (steady state)
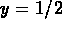. (Everything else is transient.)
- (a)
-
The model reduces to
(Note that
.)
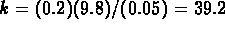The characteristic equation has roots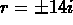 
(approximately)
and so the general solution is
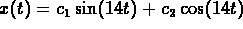. The initial data
determines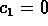 
and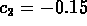 
.
- (b)
-
The period is
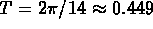and the amplitude is 
.
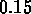The mass passes through the equilibrium position (x=0) twice during
each period and there are 133.7 periods in 60 seconds, so it passes
through equilibrium 267 times in a minute.
- (c)
-
If damping is present (and the mass still oscillates), then the
solution is of the form
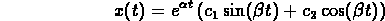
where
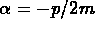and you don't care about 
.
Let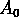 
denote the amplitude at t=0. The amplitude
(or pseudo-amplitude) at time t=60 is them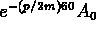 
and the data gives you the equation
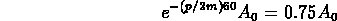
or
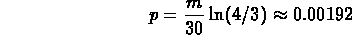
- (a)
-
The characteristic equation reduces to
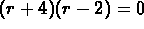so the
roots are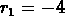 
and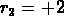 
.
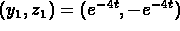The first solution pair is 
.
The second solution pair is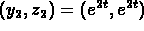 
.
(You can test linear independence with the Wronskian.)
The general solution is
.
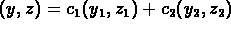- (b)
-
The initial data gives
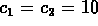and so
,
,
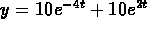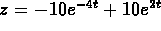A sketch of the solution curve starts at the point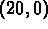 
in
the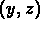 
plane and goes off to infinity approaching the
line y=z asymptotically.
(Notice that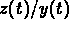 
is close to 1 for large t.)
- (c)
-
If you choose initial data so that the constants in the general
solution become
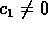and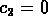 
, then you get convergence
to the origin; the solution becomes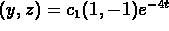 
.
(You must ``remove'' that nasty growing exponential).
Any initial data of the form 
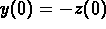works.
The solution curve in this case follows a straight line to the origin.
© 1996 by Will Brother. All rights Reserved. File last modified on April 25, 1996.