MA2051 - Ordinary Differential Equations
Review 1
1. Solve the following initial value problems.
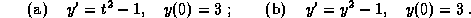
2. The Worcester Yeast Corporation grows and sells a yeast
used in beverage production. The yeast is grown in a very large vat,
where it is provided with ample nutrient for growth. Assume that,
in the absence of harvesting, the rate of growth of this yeast is proportional
to its present population and that the yeast population will double its
size in 4 hours.
- (a)
-
Derive a model for the growth of the
yeast population P (measured in kilograms)
when the yeast is harvested at a constant rate H (kg/hour).
(Note: Use the doubling time to determine the growth rate.)
- (b)
-
If the harvest rate is too large, the yeast population
will be used up in finite time (and you are out of business).
Determine the largest constant harvest rate that will not use all of
the yeast in a finite time.
What is the maximum amount of yeast that you will harvest
in an 8 hour day if the initial yeast population
is 100 kg and you use a constant harvest rate?
- (c)
-
Is it possible to harvest more yeast by using a nonconstant harvesting
policy? Justify your answer.
3.
Given that

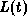 solves
solves 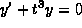 with
with 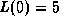 ,
,
and

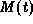 solves
solves 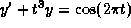 with
with 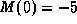 ,
,
find the solution, in terms of L and M, for
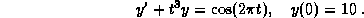
4.
Consider the following initial value problem:
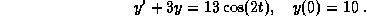
- (a)
-
Find a nontrivial homogeneous solution.
- (b)
-
Use the method of undetermined coefficients to
find a particular solution.
- (c)
-
Find the solution to the initial value problem.
- (d)
-
Describe the behavior of the solution for large values of
the independent variable t. What is the transient
component of the solution?
5.
Consider the differential equation:

- (a)
-
Find all of the steady states for this equation.
- (b)
-
Determine the regions in the
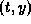 -plane where the solution
is increasing and where it is decreasing. Use this information to
sketch a solution curve for each of three different initial
points:
-plane where the solution
is increasing and where it is decreasing. Use this information to
sketch a solution curve for each of three different initial
points: 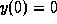 ,
, 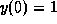 , and
, and 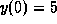 .
.
- (c)
-
Use your sketch to determine the stability of each steady state.
Justify your answer.
- (d)
-
Use one step of Euler's method to approximate the time
required for the solution to decrease
from an initial position
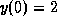 to the level
to the level 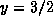 .
.
Solutions To This Review
© 1996 by Will Brother.
All rights Reserved. File last modified on March 22, 1996.
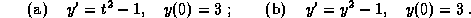
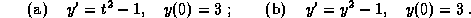

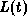 solves
solves 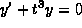 with
with 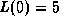 ,
,

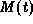 solves
solves 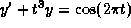 with
with 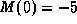 ,
,
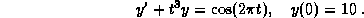
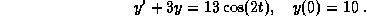

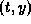 -plane where the solution
is increasing and where it is decreasing. Use this information to
sketch a solution curve for each of three different initial
points:
-plane where the solution
is increasing and where it is decreasing. Use this information to
sketch a solution curve for each of three different initial
points: 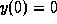 ,
, 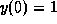 , and
, and 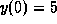 .
.
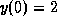 to the level
to the level 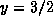 .
.