MA2051 - Ordinary Differential Equations
Review For Exam II - Solutions
REVIEW QUESTIONS
1.
This problem analyzes 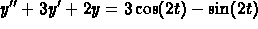 .
.
-
(a)
-
The characteristic equation is
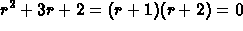 and so the roots are
and so the roots are 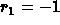 and
and 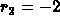 . This gives two
solutions
. This gives two
solutions 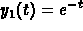 and
and 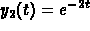 . To check
independence, compute the Wronskian and show that it is never zero.
. To check
independence, compute the Wronskian and show that it is never zero.
-
(b)
-
To find a particular solution, use the method of undetermined
coefficients and look for a solution of the form
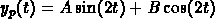 . Plug this into the
original equation and solve for A and B to obtain
. Plug this into the
original equation and solve for A and B to obtain
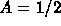 and B=0. Hence, a particular solution is
and B=0. Hence, a particular solution is
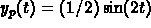 .
.
-
(c)
-
The general solution is
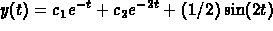 . The initial
data give you equations for
. The initial
data give you equations for 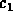 and
and 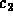 . Solving these
equations give the solution
. Solving these
equations give the solution
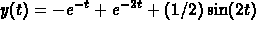 .
.
-
(d)
-
The transient component is
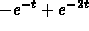 (because this is
the part that converges to zero as t goes to infinity).
This is less than
(because this is
the part that converges to zero as t goes to infinity).
This is less than 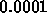 for
for 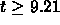 .
(Just set
.
(Just set 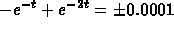 and solve for t;
it is a quadratic equation for
and solve for t;
it is a quadratic equation for 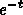 .)
.)
-
(e)
-
The limiting periodic solution (obtained in part (c)) is
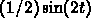 . The period is
. The period is 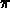 and the amplitude is
and the amplitude is 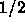 .
.
-
(f)
-
Go back to the general solution in part (c) and choose the initial
data so that
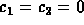 . The right choice is
. The right choice is
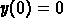 and
and 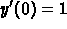 .
.
2.
The characteristic equation has roots 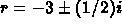 , so that
, so that
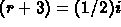 . Square both sides (
. Square both sides (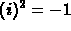 )
and simplify to obtain the
characteristic equation
)
and simplify to obtain the
characteristic equation 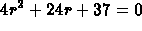 . It follows that the
original differential equation was
. It follows that the
original differential equation was 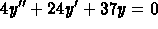 .
.
For part (b), 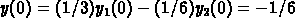 .
Similarly, with a little differentiation,
.
Similarly, with a little differentiation,
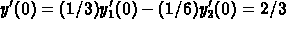 .
.
3.
This problem analyzes a spring-mass system.
-
(a)
-
The system is undamped and there is no forcing term, so
the mathematical model that you want is
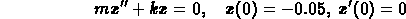
where m = 6 and k = 98.
-
(b)
-
The general solution is
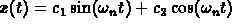 where
where 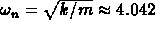 is the natural frequency
and the period is
is the natural frequency
and the period is 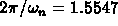 seconds.
seconds.
To find the amplitude of the motion, use the initial data to solve for
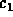 and
and 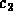 to obtain
to obtain 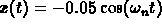 .
The amplitude is
.
The amplitude is 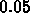 meters.
meters.
-
(c)
-
The period is
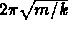 . If you increase the mass
by a factor of 4, you will double the period.
. If you increase the mass
by a factor of 4, you will double the period.
The amplitude will not change with a change in the mass. (It depends
only on the initial position in this problem.)
-
(d)
-
The new model is
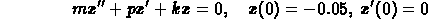
and the system will exhibit oscillations as long as the characteristic
equation has complex roots. This occurs for
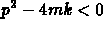 . Plug in the numbers to find that you have oscillations
for
. Plug in the numbers to find that you have oscillations
for 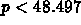 .
.
4. Solve a system of first-order equations.
-
(a)
-
The characteristic equation is
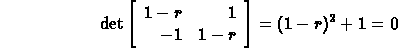
The roots are 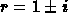 (where
(where 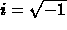 ).
The corresponding solution pairs are
).
The corresponding solution pairs are
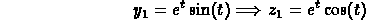
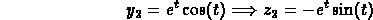
(You obtain 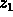 from
from 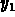 , for example, by substituting
, for example, by substituting
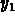 back into the first differential equation in the system.)
To verify independence, compute the Wronskian
back into the first differential equation in the system.)
To verify independence, compute the Wronskian
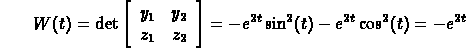
The Wronskian is never zero, so the solutions are linearly independent.
The general solution pair is
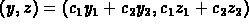 where
where 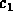 and
and 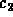 are arbitrary constants.
are arbitrary constants.
-
(b)
-
The initial data give you
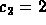 and
and 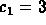 in the formula
for the general solution.
in the formula
for the general solution.
-
(c)
-
Plot a few points to obtain a spiral heading away from the origin.
-
(d)
-
Differentiate the quantity
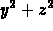 to obtain
to obtain
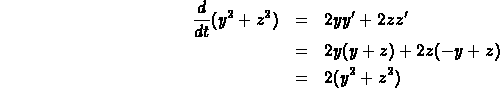
This last quantity is always positive and so, as soon as the
solution curve is away from the stationary point 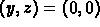 ,
its distance from the origin is strictly increasing.
,
its distance from the origin is strictly increasing.
5.
The first step is to write the second-order equation as a first-order
system:
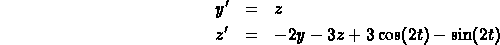
Euler's method starts with 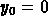 and
and 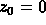 (the initial data).
Because you want the solution at t=1 and you are using
two steps,
(the initial data).
Because you want the solution at t=1 and you are using
two steps, 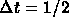 .
The next two steps are
.
The next two steps are

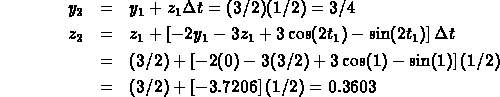
Your approximation for 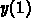 is
is 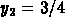 . From Problem #1,
the exact value is
. From Problem #1,
the exact value is 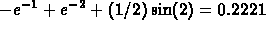 .
The absolute error is
.
The absolute error is 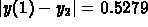 . The relative
error is
. The relative
error is 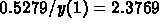 , or about 237%. (Bigerror.)
, or about 237%. (Bigerror.)

© 1996 by Will Brother.
All rights Reserved. File last modified on April 25, 1996.
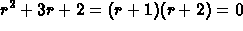 and so the roots are
and so the roots are 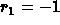 and
and 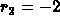 . This gives two
solutions
. This gives two
solutions 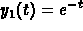 and
and 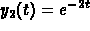 . To check
independence, compute the Wronskian and show that it is never zero.
. To check
independence, compute the Wronskian and show that it is never zero.
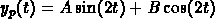 . Plug this into the
original equation and solve for A and B to obtain
. Plug this into the
original equation and solve for A and B to obtain
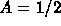 and B=0. Hence, a particular solution is
and B=0. Hence, a particular solution is
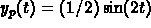 .
.
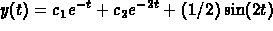 . The initial
data give you equations for
. The initial
data give you equations for 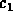 and
and 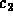 . Solving these
equations give the solution
. Solving these
equations give the solution
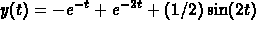 .
.
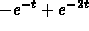 (because this is
the part that converges to zero as t goes to infinity).
This is less than
(because this is
the part that converges to zero as t goes to infinity).
This is less than 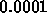 for
for 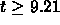 .
(Just set
.
(Just set 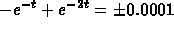 and solve for t;
it is a quadratic equation for
and solve for t;
it is a quadratic equation for 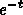 .)
.)
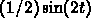 . The period is
. The period is 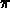 and the amplitude is
and the amplitude is 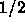 .
.
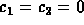 . The right choice is
. The right choice is
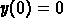 and
and 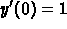 .
.
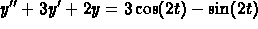 .
.
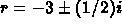 , so that
, so that
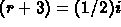 . Square both sides (
. Square both sides (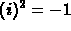 )
and simplify to obtain the
characteristic equation
)
and simplify to obtain the
characteristic equation 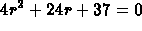 . It follows that the
original differential equation was
. It follows that the
original differential equation was 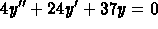 .
.
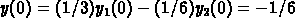 .
Similarly, with a little differentiation,
.
Similarly, with a little differentiation,
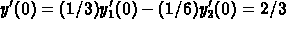 .
.
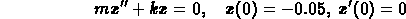
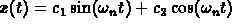 where
where 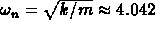 is the natural frequency
and the period is
is the natural frequency
and the period is 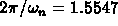 seconds.
seconds.
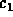 and
and 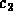 to obtain
to obtain 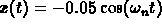 .
The amplitude is
.
The amplitude is 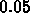 meters.
meters.
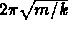 . If you increase the mass
by a factor of 4, you will double the period.
. If you increase the mass
by a factor of 4, you will double the period.
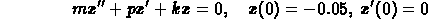
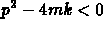 . Plug in the numbers to find that you have oscillations
for
. Plug in the numbers to find that you have oscillations
for 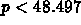 .
.
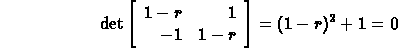
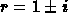 (where
(where 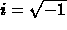 ).
The corresponding solution pairs are
).
The corresponding solution pairs are
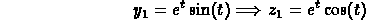
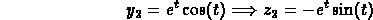
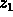 from
from 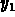 , for example, by substituting
, for example, by substituting
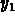 back into the first differential equation in the system.)
To verify independence, compute the Wronskian
back into the first differential equation in the system.)
To verify independence, compute the Wronskian
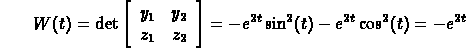
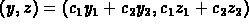 where
where 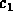 and
and 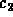 are arbitrary constants.
are arbitrary constants.
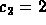 and
and 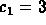 in the formula
for the general solution.
in the formula
for the general solution.
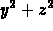 to obtain
to obtain
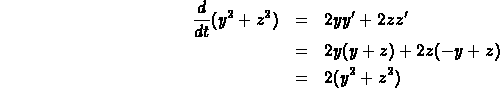
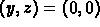 ,
its distance from the origin is strictly increasing.
,
its distance from the origin is strictly increasing.
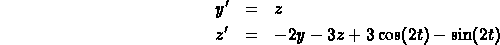
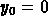 and
and 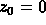 (the initial data).
Because you want the solution at t=1 and you are using
two steps,
(the initial data).
Because you want the solution at t=1 and you are using
two steps, 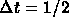 .
The next two steps are
.
The next two steps are

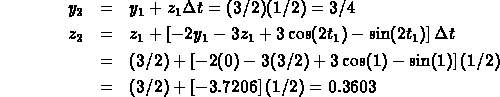
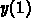 is
is 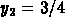 . From Problem #1,
the exact value is
. From Problem #1,
the exact value is 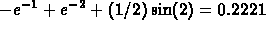 .
The absolute error is
.
The absolute error is 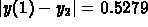 . The relative
error is
. The relative
error is 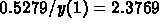 , or about 237%. (Bigerror.)
, or about 237%. (Bigerror.)
