MA 2611 E '98 Test 2

1.

A check of the 1998 opening day rosters of 29 of the 30 major league baseball teams shows that 117 of the 403 pitchers are left-handed.

a.

(10 points) Suppose the 403 pitchers constitute a random sample from a large population having a proportion p of left-handers. Use the given data to obtain a point estimate of p.

ANS: $\hat{p}=117/403=0.29$.

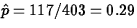b.

Use the given data to obtain an approximate 95% confidence interval for p. Be sure to check any assumptions you need.

ANS: First, the normal approximation is valid since both 117 and 403-117 are well above 10. (5 points)
Since

$$\hat{\sigma}(\hat{p})=\sqrt{\frac{(0.29)(0.71)}{403}}=0.0226,$$

The interval is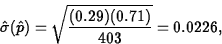

$$0.29\pm (1.96)(0.0226)=(0.246,0.334).$$

(5 points)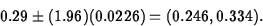

c.

(5 points) Explain what 95% confidence means in terms of the interval you generated in part b.

ANS: If we repeatedly sample from the population and construct a 95% confidence interval for each sample, then approximately 95% of all intervals will contain the true p.

d.

(10 points) According to Grolier's Encyclopedia, approximately 10% of adults are left-handed. In terms of handedness, do you think these pitchers represent a random sample from the adult population? Support your answer using the results of part b.

ANS: No, since 0.1 is not in the interval.

2.

(20 points) A machine crimps bottle caps on bottles of clam juice. Suppose the probability the crimp is defective on any given bottle is 0.01, independently of whether the crimp is defective or not on any other bottle. Suppose the random variable N is the number of bottles until the first defective crimp (including the defective one). What is the probability mass function of N? (Hint: the probability the first bottle has a defective crimp is 0.01. The probability the second bottle is defective is $0.99\times 0.01=0.0099$because the first bottle is not defective, and the second one is, and these events are independent.)

ANS: $p_N(n)=(0.01)(0.99)^{n-1},~n=1,2,\ldots$.

3.

A continuous random variable Y has density

a.

(10 points) Sketch a graph of the density.

b.

(10 points) Find the probability Y is less than 1/4.

ANS:

$$P(Y<1/4)=\int_{-\infty}^{1/4}p_Y(y)dy=\int_{-1}^0(1+y)dy+ \int_0^{1/4}(1-y)dy=23/32.$$

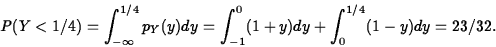
c.

Find the mean and variance of Y.

ANS: E(Y)=0, by symmetry. (5 points)
Therefore,

$$\sigma^2_Y=\int_{-\infty}^\infty y^2p_Y(y)dy=\int_{-1}^0 y^2 (1+y)dy+ \int_0^1 y^2 (1-y)dy=1/6.$$

(5 points)

4.

(5 points) Leonardo claims that his research shows a Pearson correlation of 0.35 between religious affiliation (Roman Catholic, Protestant, Jewish, Other or None) and party affiliation (Republican, Democrat, Other or None) among U.S. voters. Do you agree that this is possible? Why or why not?

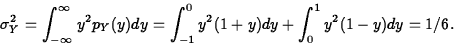
ANS: This is not possible since Pearson correlation is only applicable to quantative, not categorical, variables.

5.

In a study on Federal land ownership, data obtained for 49 of the 50 states include the total land area of each state (in acres) and the number of acres of Federally-owned land in the state. A regression analysis is conducted in which the natural log of the number of acres of Federally-owned land (L_FEDLAN) in a state is regressed on the natural log of the total acres of land area in the state (L_STATEL). SAS/INSIGHT regression output is shown in Figure 1, and Studentized residual plots are shown in Figure 2.

a.

What is the response? The predictor? The regressor?

ANS: The response is L_FEDLAN. The predictor is the total acres of land area, STATELAND. The regressor is L_STATEL. (5 points each)

b.

Write out the equation of the fitted model. Interpret each estimated parameter.

ANS: The fitted model is

$$\widehat{L\_FEDLAN}=-5.9657+1.3338\cdot L\_STATEL.$$

(5 points)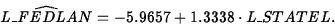
The slope, 1.3338, is the change in predicted L_FEDLAN per unit change in the regressor, L_STATEL. In terms of the predictor, it is

$$1.3338=\frac{d \widehat{L\_FEDLAN}}{d STATELAND}STATELAND.$$

(5 points for either)
The intercept does not have an interpretation of its own. (5 points)

c.

(5 points) By what proportion is the uncertainty in predicting the response reduced by using the regression model?

ANS: r²=0.6038.

d.

(5 points) What is the correlation between L_FEDLAN and L_STATEL?

ANS: $r=\sqrt{0.6038}=0.7770$.

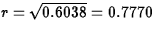e.

Evaluate the fit using the Studentized residuals.

ANS: The Studentized residuals look reasonably normal. (5 points)
The plot of Studentized residuals versus L_STATEL shows a pattern: high values at both low and high L_STATEL values, and low values at middle L_STATEL values. (5 points)

f.

(5 points) Estimate the standard deviation of the random errors.

ANS: $\hat{\sigma}=\sqrt{MSE}=1.2863$.

6.

Flexible circuit boards shrink during processing, and a a result have to be cut large to compensate. A production engineer wants to obtain a range of values which she is 95% confident will contain at least 99% of the shrinkages of the boards manufactured by her company. A sample of 50 boards have a mean percent shrinkage of $9.183\times 10^{-3}$ with a standard deviation of $2.250\times 10^{-3}$. The data show no evidence of non-normality.

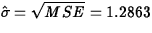a.

(10 points) What kind of interval should the engineer obtain?

ANS: A normal-theory tolerance interval with L=0.95 and $\gamma=0.99$.

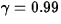b.

(10 points) Calculate the interval for these data.

ANS: $[9183\pm (3.126)(2.250)]\times 10^{-3}=(2.1495\times 10^{-3},16.2165\times 10^{-3})$.

 

Figure 1:   Regression output for problem 5

 

Figure 2:   Studentized residual plots for problem 5