MA 2611 A' 96 Test 2

1.

(40 points) It may seem counterintuitive, but the distribution of the first significant (i.e., non-zero) digit in many collections of numbers is not uniform on the integers 1 through 9, but rather follows Benford's distribution, which has probability mass function

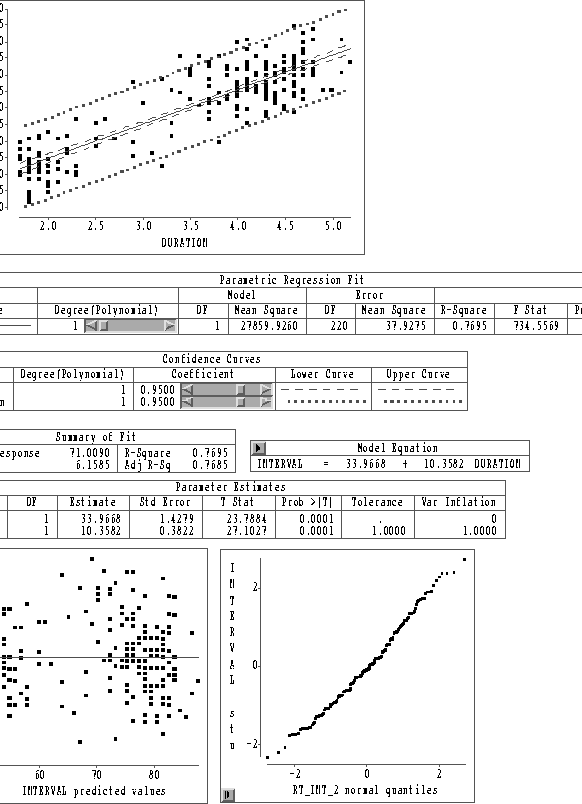
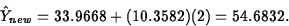Thus, for example, according to Benford's distribution, the probability that the first significant digit of a randomly chosen number is an 8 is

One use of this distribution is in auditing financial records. The idea is that if the books have been artificially altered, the distribution of the first significant digit will differ markedly from what is predicted by Benford's distribution. Suppose the IRS is auditing the financial records of a large company.

a.

If the numbers in the company's records follow Benford's distribution, what is the probability that a randomly chosen number from the company's records has first significant digit equal to 1?

ANS: $p_X(1)=\log_{10}(1+\frac{1}{1})=\log_{10}(2)=0.301.$

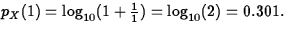
b.

If the IRS randomly samples 1000 numbers from the company's records (which contain billions of numbers), and if these numbers follow Benford's distribution, approximately what is the distribution of Y, the number of the 1000 numbers having first significant digit equal to 1?

ANS: $Y\sim b(1000,0.301)$

c.

Suppose 258 of the 1000 numbers in the IRS sample have first significant digit equal to 1. Is this convincing evidence that the company's financial records do not follow Benford's law? Show your reasoning.

ANS:

$$P(Y\leq 258)=P(Y\leq 258.5)= P\left(\frac{Y-301}{\sqrt{1000(... ...\sqrt{1000(0.301)(0.699)}}\right) \doteq P(Z\leq -2.93)=0.0017.$$

This is convincing evidence, since if the records follow Benford's law, we have observed a very rare (17/10000) occurrence.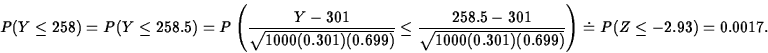

It is also acceptable to construct a 95% confidence interval for p, the population proportion of numbers having first digit 1. This interval turns out to be (0.231,0.285), which, since it doesn't contain 0.301, suggests that the data do not follow Benford's distribution.

2.

(20 points) Low frequency impedence (LFI) is a method for testing green-state (i.e. pre-sintering) powder metallurgy parts for microscopic flaws. In LFI, current is injected into a grid of probes on the part surface and the voltage differences between probes are recorded. The voltage differentials of flawed parts will have a different distribution than those of good parts. Assume the measured differential voltages between two specific probes for a sample of 16 good parts have a sample mean of 0.75 volts with a sample standard deviation of 0.1 volts. The data appear normally distributed and there are no outliers.

a.

Use these data to obtain an interval that with 95% confidence will contain the differential voltage reading of a new good part.

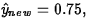
ANS: 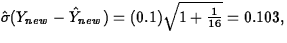$\hat{y}_{new}=0.75,$$\hat{\sigma}(Y_{new}-\hat{Y}_{new})=(0.1)\sqrt{1+\frac{1}{16}}= 0.103,$t_15,0.975=2.1314. The interval is $0.75 \pm (0.103)(2.1314)=(0.53,0.97)$

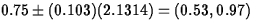
b.

A new part of the same type is now tested and shows a differential voltage reading of 1.30 volts. What do you conclude about the quality of this part?

ANS: Since it lies outside the prediction interval, we conclude it is flawed.

3.

(40 points) Recall that earlier in the term we looked at a set of eruption times for the Old Faithful geyser. For these same data, Figure 1 is SAS/INSIGHT output for the regression of the interval between eruptions on the duration of the previous eruption. The National Park Service hopes to use these data to better predict the times until the next eruption.

a.

What proportion of the variation in the intervals between eruptions is explained by the regression?

ANS: r²=0.7695

b.

Write the equation of the fitted model. Interpret the slope of this equation. Does the intercept have a meaningful interpretation of its own? If so, what is it? If not, why not?

ANS:

$$\widehat{INTERVAL}=33.9968+10.3582\cdot DURATION.$$

The slope is the change in predicted INTERVAL per unit change in DURATION. The intercept has no meaning of its own. If it did, it would be the predicted time until the next eruption when the present eruption lasts 0 minutes.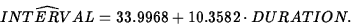

c.

Using graphs and/or measures on the output, assess the quality of the model fit.

ANS: The fit looks good. The normal quantile plot of the Studentized residuals is straight and the residuals are randomly scattered versus fitted values. There are clearly still two groups of eruptions, but the line summarizes both well. r² is nearly 0.77, which means that 77% of the variation in the time until the next eruption is explained by knowing the duration of the current eruption.

d.

There are 5 lines superimposed on the plot of interval versus duration. The center line is the fitted regression line. The two lines nearest the fitted regression line are 95% confidence limits for the mean response. The outer two lines delimit a 95% prediction interval for the interval between eruptions at each duration. The duration of the last eruption was 2 minutes. Predict the time from the last eruption until the next eruption. Use the information contained in the plot to give an approximate 95% prediction interval for this time.

ANS:

$$\hat{Y}_{new}=33.9668+(10.3582)(2)=54.6832.$$

The actual interval is (42.46,66.91). Any student answers that are reasonably close to this are acceptable.

 

Figure 1:   SAS/INSIGHT output for interval between eruptions of Old Faithful regressed on duration of the last eruption.