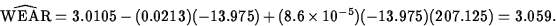next up previous


MA 2612 Test 3 D '98







NAME:





1.
Ray Bob says he can't decide between two MLR models for the same set of data. He says that he likes large R2a and small MSE, but that model 1 has a larger R2a than model 2, but also a larger MSE. What do you say to Ray Bob?

ANS: This can't be true, because $R^2_a=1-\mbox{MSE}/S^2$ (see book, p. 474). Since S2 is the same regardless of model, a model with larger R2a must have smaller MSE.

2.
An experiment was conducted to determine the effect of miles driven and temperature on tire wear. Thirty-two tires of the same model were randomly assigned to temperature and distance settings. They were then subjected to simulated driving at the assigned temperature and distance. At the end of the driving period, the tire wear was recorded. The response is a measure of tire wear.

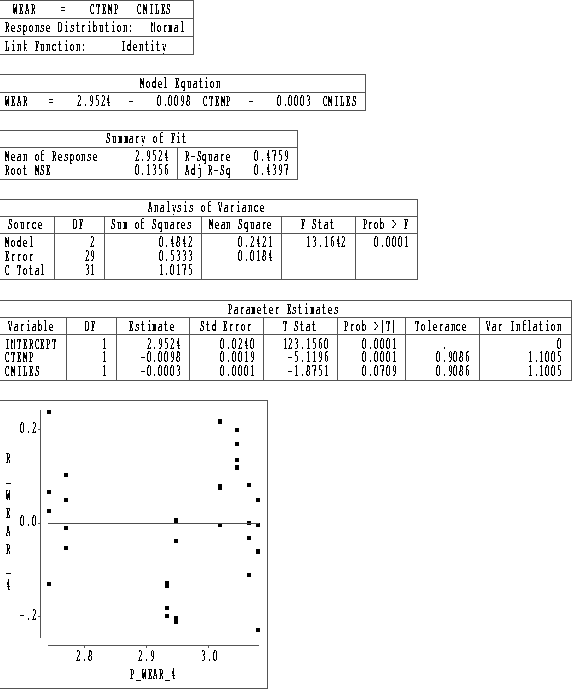
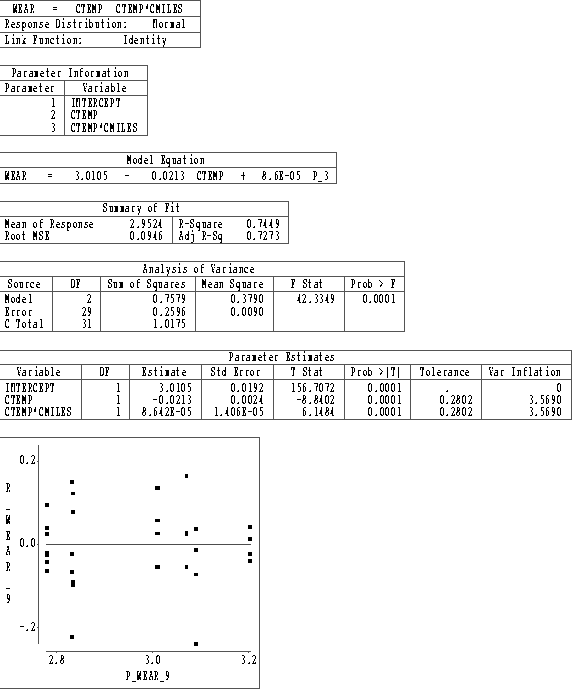
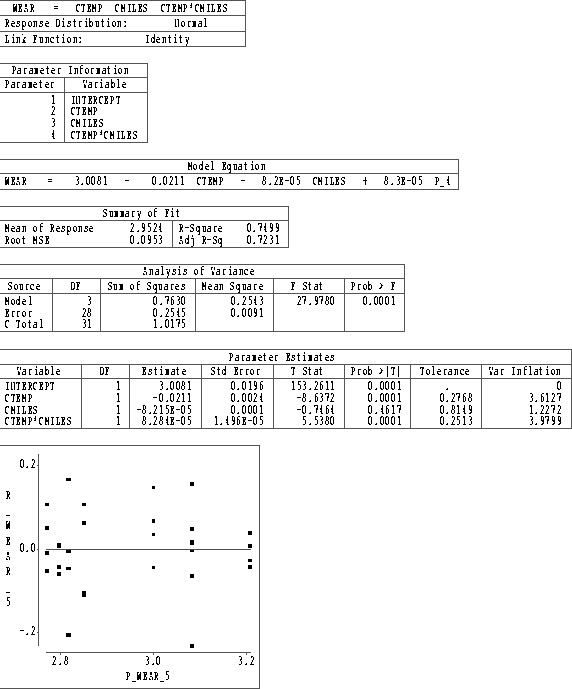
Figures 1-3 contain SAS/INSIGHT output for three fits to these data. CTEMP and CMILES are the centered predictors temperature and miles driven.

(a)
Compare the three models based on all relevant measures and graphs. Which do you think provides the best fit? Why?

Model    
Measure 1 2 3
Residual versus Under-predicts Good Good
fitted plot center values    
R2 0.4759 0.7449 0.7499
R2a 0.4397 0.7273 0.7231
MSE 0.0184 0.0090 0.0091

ANS: Based on the above measures, model 2 is best, closely followed by model 3. Model 1 is very bad.

(b)
Write out the equation for the best fitting model. Interpret this equation in terms even Professor P. can understand.

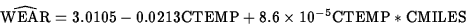
\begin{displaymath} \widehat{\mbox{WEAR}}=3.0105-0.0213 \mbox{CTEMP}+ 8.6\times10^{-5}\mbox{CTEMP}*\mbox{CMILES}\end{displaymath}

The intercept, 3.0105, is the estimated mean wear when temperature and miles are at their means.

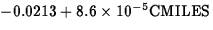The estimated change in mean wear per unit increase in temperature is $-0.0213+8.6\times10^{-5}\mbox{CMILES}$.

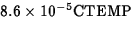The estimated change in mean wear per unit increase in miles is $8.6\times10^{-5}\mbox{CTEMP}$.

(c)
What proportion of the total variation in the tire wear measurement is explained by using the best fitting model?

ANS: 0.7449

c.
You are going on a trip of 400 miles this weekend, and you think the temperature will be 58o F. Use the best fitting model to predict your tire wear. The mean of the miles driven variable in the data set is 192.875, and that of the temperature variable is 71.975.

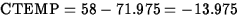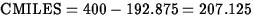ANS: $\mbox{CTEMP}=58-71.975=-13.975$, and $\mbox{CMILES}=400-192.875=207.125$, so the prediction is

\begin{displaymath} \widehat{\mbox{WEAR}}=3.0105-(0.0213)(-13.975)+ (8.6\times10^{-5})(-13.975)(207.125)=3.059.\end{displaymath}


 
Figure 1:   Regression output for model 1, problem 2
\begin{figure} \centerline{ \psfig {file=t2p2a_3.eps,height=6in,width=5in} } \vspace{2ex}\end{figure}


 
Figure 2:   Regression output for model 2, problem 2
\begin{figure} \centerline{ \psfig {file=t2p2a_4.eps,height=6in,width=5in} } \vspace{2ex}\end{figure}


 
Figure 3:   Regression output for model 3, problem 2
\begin{figure} \centerline{ \psfig {file=t2p2a_5.eps,height=6in,width=5in} } \vspace{2ex}\end{figure}

About this document ...

This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)

Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.

The command line arguments were:
latex2html -split 0 oldtest3soln.

The translation was initiated by Joseph D Petruccelli on 12/2/1999

next up previous
Joseph D Petruccelli
12/2/1999