- a.
- (10 points) Explain why this is not a
completely random design.
ANS: It is a RCBD because all five houses are assessed by each assessor. The houses are blocks.
- b.
- (10 points) Write out the model for this
problem. Explain what each parameter means.
ANS: The model is the additive RCBD model
where Yij is the assessed value given by assessor i to house j,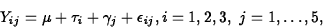
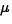is the overall population mean, 
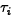is the effect due
to assessor i,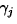 
is the effect of house j, and
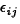is random error.
- c.
- (10 points) The macro RCBD output the
following information, as well as
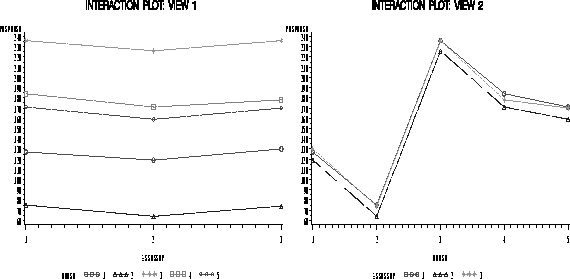
Figure 1. What do these tell you about the
suitability of the model?
TUKEYS TEST FOR ADDITIVITY: F STATISTIC: 604E-7 DEGREES OF FREEDOM: 1 7 P-VALUE: 0.994
ANS: The interaction plots show no evidence of interaction, since all line segments profiles are close to parallel. Tukey's test confirms this, as the large p-value shows.
- d.
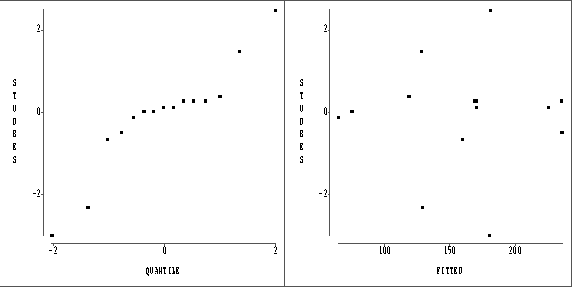
- (5 points) Figure 2 shows plots
of studentized residuals versus Student's t quantiles and fitted
values. Do these indicate a problem with the model? Give your reasons.
ANS: There is no evidence of a pattern in the plot of studentized residuals versus fitted values. The normal plot has some nonlinearity in both tails, which may indicate some nonnormality.
- e.
- (10 points) The following is the ANOVA table
for the fitted model. Are there significant differences in house
valuations among assessors? Does it appear blocking was useful?
Support your answers.
Analysis of Variance Source DF Sum of Squares Mean Square F Stat Prob > F Assessor 2 356.1 178.1 63.22 0.0001 House 4 43852.7 10963.2 3892.25 0.0001 Error 8 22.5 2.8 C Total 14 44231.3 ANS: There appear to be significant differences among assessors (p-value: 0.0001). Blocking appears to be useful (p-value: 0.0001).
- f.
- (15 points) Property taxes are based on
assessments made by these assessors. If you own a house in
the town, who do you want assessing your house, or doesn't it
matter? The town manager lives in another town, so her taxes
are not affected by which assessors are used. However, the
town budget, including the budget of the town manager's office,
is affected. Who does she want to hire as assessor, or
doesn't it matter? Justify your answers based on the SAS
output below.
General Linear Models Procedure Tukey's Studentized Range (HSD) Test for variable: Y NOTE: This test controls the type I experimentwise error rate. Alpha= 0.05 Confidence= 0.95 df= 8 MSE= 2.816667 Critical Value of Studentized Range= 4.041 Minimum Significant Difference= 3.033 Comparisons significant at the 0.05 level are indicated by '***'. Simultaneous Simultaneous Lower Difference Upper ASSESSOR Confidence Between Confidence Comparison Limit Means Limit 1 - 3 -2.033 1.000 4.033 1 - 2 7.767 10.800 13.833 *** 2 - 3 -12.833 -9.800 -6.767 ***ANS: You want either 1 or 3, since they are essentially equivalent, statistically, and both assess significantly lower than 2, on average. The town manager wants assessments high, so she will want to hire assessor 2.
