In this project you will consider the important problem of minimizing the cost of producing a given amount of electrical power from a group of non-identical generators. This is a problem faced by utility companies every day, as changes in consumer demand force them to generate more or less power. The model we will use is a relatively simple one and does not take into account the various complications that can arise due to environmental or other long-term considerations.
Consider first a single power plant. The total cost of operation
includes fuel, maintenance, and labor costs, but we will assume that
changes in output are relatively small, so that fuel cost is the only
important one. If we let P stand for the power output in megawatts
(MW) and C be the fuel cost, then Fig. 
shows a
typical curve of cost versus power output.
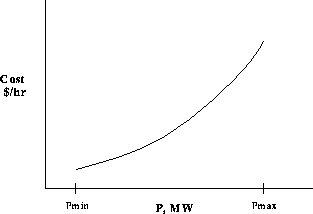
Figure: Typical Fuel-Cost curve for a single
power plant
Note that the cost curve is increasing and concave upward. In practice, a quadratic polynomial is often used to fit fuel-cost data. Note also that there are minimum and maximum values of P, Pmax and Pmin, corresponding to feasible limits of operation of the plant. The need for an upper limit should be clear; a given plant can't produce more power than it is designed for. The lower limit usually comes from thermodynamic and/or practical considerations, e.g. the fuel burning rate has to be above a certain value or the flame goes out.
Now, consider a set of m power generating stations. For each value
of i,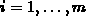 
, we have a
power output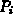 
and associated cost function 
,
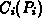corresponding to the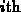 
power generating plant. Suppose that
the total power demand to be served by these power
stations is given by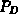 
. The the economic dispatch problem is
to minimize the total cost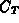 
, given by
subject to the constraints
and
That is, one has to find values of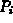 
, 
satisfying
the constraints such that the total cost is a minimum.
This problem is actually a very simplified version of the real thing. Besides the assumptions already mentioned above, this model makes the following additional assumptions.
The following exercises are intended to guide you in working through
this project. In particular, answers to the second and third exercises
below must be included in the Background section of your report
and the answers to the remaining questions should appear in the
Procedure section. Data to be used in answering some of the questions
appears in Table . Your report should not be simply answers to
the questions. Rather it should be contain a general approach to the
economic dispatch problem with and without constraints.
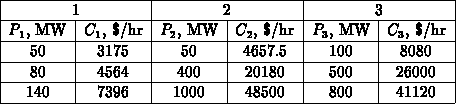
Table: Power generation - cost data for three
power plants.
find the values of 
, 
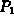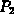, and 
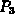that minimize the total
cost for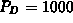 
.
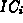, of the 
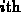power
station is defined by
For the case that the upper operating limits can be ignored, show in
general that the critical point of the cost function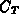 
occurs when
all of the incremental costs are equal. Explain why this result makes
sense from a qualitative point of view.
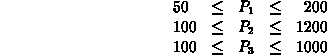
Find the values of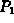 
, 
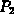, and 
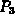that minimize the total
cost for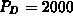 
.
?
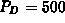