According to a recent article in Popular Mechanics![]() , the construction of
roller coasters with loops is responsible for a resurgence of
popularity for these amusements; loops are also implicated in several
deaths. In this project, you will investigate some of the crucial
aspects of roller coaster design.
, the construction of
roller coasters with loops is responsible for a resurgence of
popularity for these amusements; loops are also implicated in several
deaths. In this project, you will investigate some of the crucial
aspects of roller coaster design.
One of the first companies to produce a coaster with a loop was Schwarzkopf GmbH of Germany. The so-called Schwarzkopf loop is described in the article as follows.
Sixty-three-year-old former cartwright Anton Schwarzkopf holds nearly 60 patents in the field of roller coaster design and manufacturing, and has produced more than 55 roller coaster systems around the world. His loop is the result of rigorous research and development conducted in the early '70s at his Bavarian test track. Other roller coaster makers had designed loops, but their ``geometry'' had imposed too many Gs on passengers, resulting in whiplash, broken collar bones, bruises , and other bodily strains. Schwarzkopf determined that a safe loop consisted of a spiral in which the radius of curvature decreased at a constant rate. Thus, most modern loops are tear-drop or oval-shaped, which means riders are subjected to slightly less than 6 Gs as the roller coaster's cars enter and leave the loop.
The key phrase in the passage above is ...radius of curvature decreased at a constant rate, at least as far as this project is concerned. In general terms, your first task is to find out what radius of curvature means and why it is important in coaster design. The second task is to investigate the Schwarzkopf loop. Can you come up with a model that retains the essential features, but is simple enough that you can solve it?
To do this project, you will have to read and understand the material
in §14.4 and 14.5 in the text. This is where the unit tangent and
normal vectors 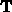 and
and 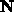 of a curve are described, as
well as the notion of a the curvature,
of a curve are described, as
well as the notion of a the curvature, 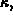 of a curve.
of a curve.
In designing a roller coaster, the most important concepts are speed and force. You want the speed to be high, but not too high and the same goes for the forces on the passengers. According to the article quoted above, the total acceleration should not exceed 6 Gs. Obviously, we don't have a test track in Bavaria, so we will have to construct a simplified mathematical model. Here is the first set of assumptions.
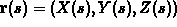 in three dimensions parametrized by s. Here s is
arc-length along the curve.
in three dimensions parametrized by s. Here s is
arc-length along the curve.
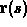 . This assumption means that we won't be
able to account for internal forces on the passengers or for torques
caused by the car having a finite height. These are certainly
important aspects of roller coaster design, but they are way beyond
the scope of what we are trying to do.
. This assumption means that we won't be
able to account for internal forces on the passengers or for torques
caused by the car having a finite height. These are certainly
important aspects of roller coaster design, but they are way beyond
the scope of what we are trying to do.
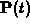 , on the track can be
represented by a ``speed function''
, on the track can be
represented by a ``speed function'' 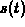 , so that we have
, so that we have
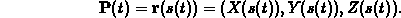
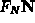 and
gravity
and
gravity  .
.
Under these assumptions, Newton's second law and the decomposition
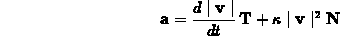
can be used to obtain the two scalar equations
Equation ![]() is a differential equation that will have to be
solved for the speed function
is a differential equation that will have to be
solved for the speed function 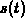 . Equation
. Equation ![]() allows one
to compute the normal acceleration,
allows one
to compute the normal acceleration, 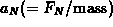 if you
know the curvature
if you
know the curvature  and the
speed
and the
speed 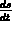 . It wasn't made explicit in the equations, but
. It wasn't made explicit in the equations, but
 ,
, 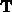 ,
, 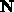 , and
, and 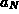 all depend on time because
the car is moving along the curve and
all depend on time because
the car is moving along the curve and  ,
, 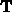 , and
, and 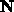 all change as the car moves.
all change as the car moves.
Here are some specific things I want to see in your report, as part of the usual Introduction, Background, Procedure, and Conclusion structure. The next section of this handout provides hints and clues that should aid your investigations. You also might want to do some research in the library, including past MQPs.
 ,
, 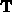 , and
, and 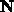 vary
along your loop.
vary
along your loop.
Here are some suggested activities, designed to help you construct and analyze your own ``Schwarzkopf loop''.
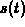 and evaluate
and evaluate
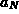 in these special cases. For a straight line, the answer should
be yes. For a circle, look up the simple pendulum equation in your
Physics book.
in these special cases. For a straight line, the answer should
be yes. For a circle, look up the simple pendulum equation in your
Physics book.
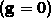 ? How would that simplify your
computations?
? How would that simplify your
computations?
 as a function of s?
as a function of s?
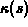 , can you find a plane curve
, can you find a plane curve 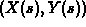 that has this
curvature? The answer is yes, and I suggest you study the curve
defined by
that has this
curvature? The answer is yes, and I suggest you study the curve
defined by
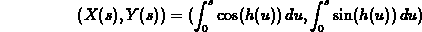
where, hopefully, the function 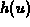 can be related to the curvature
can be related to the curvature
 in some simple fashion. Try to generalize to a curve in three
dimensions.
in some simple fashion. Try to generalize to a curve in three
dimensions.
This is an open-ended project. That means, for one thing that there is no unique ``right'' answer. Here is what I think is a reasonable schedule for the completion of this project.