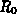You have just started a co-op position with the BiggGlass company, manufacturers of fine household glassware. The head of the company, Mr. Bigg, walks into your cubicle and tells you that consumers are complaining that BiggGlass' glasses spill too easily. He then says that you have to fix it, and walks out.
You are feeling a little overwhelmed, so you go down the hall to talk to your immediate supervisor, Dr. T. Integral. He tells you that most of the consumer complaints say that they tilt the glass to begin drinking, only to have the liquid unexpectedly come over the rim and down their chins. He suggests that maybe the problem is the geometry of the glass, which is a fairly short cylinder. He suggests that you study the following problems and write a report describing your work and containing a recommendation for changing the design. He also warns you in advance that Mr. Bigg will not accept any results not supported by careful analysis and triple integrals.
Suppose that the interior of a glass is in the form of a cylinder of
radius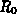 
and height H. The glass is placed on a level surface
and filled to a height h with liquid, as shown in
figure 
below.
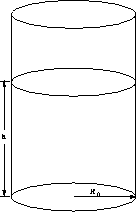
Figure: BiggGlass glass on a level surface
Now, suppose that the glass is tipped at an angle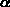 
, measured
from the vertical axis. Then the liquid height, measured along
the glass from the bottom, increases on one side and decreases on the
other, as shown in figure below.
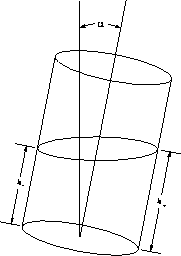
Figure: BiggGlass glass tilted at an angle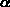 
.
The minimum and maximum distances are labeled as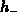 
and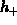 
in
the figure. Find how these quantities depend on the angle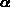 
and
the glass radius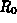 
. You may assume that the surface of the liquid
is flat, and neglect any effects due to surface tension.
Repeat the investigations of the first problem, but for a glass that is conical instead of cylindrical. That is, the lateral surface of the glass is described by the following equation in cylindrical coordinates,
where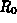 
is the radius of the base and the positive constant b
determines how much the glass radius increases with increasing z.
Dr. Integral tells you that your first priority must be to solve the first problem and write it up carefully. The second problem is more of a challenge problem. If you can solve it, however, he promises that the company will reward you handsomely.