Next: About this document ...
Up: lab_template
Previous: Exponentials and Logarithms
Subsections
Consider the functions 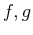 defined by
defined by
To be able to get an inverse the function must be one-to-one. You can plot the functions to get a hint as to whether they are invertible or not.
> f:=x->exp(x)+exp(-x);
> plot(f(x),x=-5..5);
> g:=x->exp(x)-exp(-x);
> plot(g(x),x=-5..5);
Both satisfy the vertical-line test but 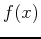 is not invertible since it does not satisfy the horizontal-line test. Indeed
is not invertible since it does not satisfy the horizontal-line test. Indeed 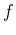 is not one-to-one, for instance
is not one-to-one, for instance
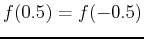 . From the plot it seems that the function
. From the plot it seems that the function 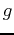 is one-to-one. In order to determine its inverse we solve for x.
is one-to-one. In order to determine its inverse we solve for x.
> solve(g(x)=y,x);
We observe that one of the solutions is not defined since the arguement of the logarithm can only be positive. Thus:
> ginv:=y->ln(y/2+sqrt(y^2+4)/2);
Let's look at the plot along with the line 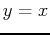 to see if our functions seem to make sense.
to see if our functions seem to make sense.
> plot({x,g(x),ginv(x)},x=-20..20,y=-20..20,scaling=constrained);
Let's check that we have computed the right inverse. By definition the composotion of the functions should be the line 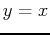 since an inverse is the reflection about this line.
since an inverse is the reflection about this line.
> g(ginv(y));
> simplify(g(ginv(y)));
> ginv(g(x));
> simplify(ginv(g(x)));
We are having difficulty getting 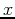 for the last composition. Again, the logarithm can't have a negative arguement and the computer knows this. To find the variable values that will work solve
for the last composition. Again, the logarithm can't have a negative arguement and the computer knows this. To find the variable values that will work solve 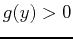 . You may come across this in the exercises.
. You may come across this in the exercises.
> solve(g(y)=0,y);
So, you need to let the computer know that the variable will only be 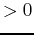 .
.
The simple model for growth is exponential growth, where
it is assumed that
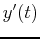 is proportional to
is proportional to 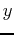 . That is,
. That is,
Separating the variables and integrating (see section 4.4 of the text),
we have
so that
In the case of exponential growth, we can drop the absolute value
signs around 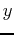 , because
, because 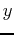 will always be a positive quantity.
Solving for
will always be a positive quantity.
Solving for 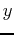 , we obtain
, we obtain
which we may write in the form 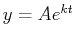 , where
, where 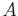 is an
arbitrary positive constant.
is an
arbitrary positive constant.
In a sample of a radioactive material, the
rate at which atoms decay is proportional to the amount of material present.
That is,
where 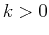 is a constant. This is the same equation as in exponential growth,
except that
is a constant. This is the same equation as in exponential growth,
except that 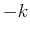 replaces
replaces 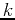 . The solution is
. The solution is
where 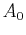 is a positive constant. Physically,
is a positive constant. Physically, 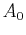 is the amount of
material present at
is the amount of
material present at 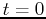 .
.
Radioactivity is often expressed in terms of an element's half-life.
For example, the half-life of carbon-14 is 5730 years. This statement means
that for any given sample of
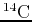 , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is 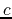 years, it must be
that
years, it must be
that
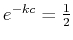 , so that
, so that 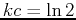 and
and
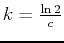 .
.
- For each function given below
- a
- Plot the function over the interval
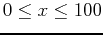 . Which functions are not invertible and why?
. Which functions are not invertible and why?
- b
- Find the inverse of the invertible function(s) and plot the function and its inverse along with the line
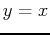 on the intervals
on the intervals
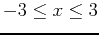 .
.
- c
- Show that you have the correct inverse by using the composite definition.
- Suppose that the population of a certain bacteria can be modeled by an exponential function. In a particular experiment, the number of bacteria was
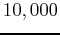 at
at 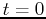 . Four hours later, the bacteria was
. Four hours later, the bacteria was 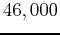 . Find the value of the growth constant
. Find the value of the growth constant 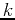 and use it to predict the number of bacteria that would have been present after
and use it to predict the number of bacteria that would have been present after 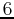 hours.
hours.
- How long would it take for half of 75 grams of a radioactive element to decay if it decays at a yearly rate of 2.2%.



Next: About this document ...
Up: lab_template
Previous: Exponentials and Logarithms
Dina J. Solitro-Rassias
2018-10-03
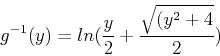
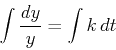
![]() , after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is
, after 5730 years, half of it
will have undergone decay.
So, if the half-life is of an element Z is ![]() years, it must be
that
years, it must be
that
![]() , so that
, so that ![]() and
and
![]() .
.